DIFFERENCE QUOTIENT METHOD TO FIND INSTANTANEOUS RATE OF CHANGE

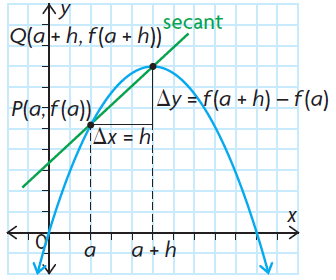
If P(a, f(a)) and Q(a + h, f(a + h)) are two points on the graph of y = f(x) then the instantaneous rate of change of y with respect to x at P can be estimated using 

𐤃y/𐤃x = [f(a + h) - f(a)] / h

where h is very small number. This expression is called difference quotient 

Problem 1 :

For the function f(x) = 6x² - 4, estimate the instantaneous rate of change for the given values of x.

a) x = -2     b)  x = 0      c) x = 4      d) x = 8

Solution :

a) Write the difference quotient for the average rate of change in volume as the side length changes between 2 and any value

𐤃y/𐤃x = [f(a + h) - f(a)] / h

f(x) = 6x² - 4

f(-2) = 6(-2)² - 4

= 6(4) - 4

= 24 - 4

= 20

[f(-2 + h) - f(-2)] / h = [(6(-2 + h)² - 4) - 20] / h

= [6(-2 + h)² - 24 - 20] / h

= [6(-2 + h)² - 44] / h

Applying h = 0.01

= [6(-2 + 0.01)² - 44] / 0.01

= [6(-1.99)² - 44] / 0.01

= [6(3.9601) - 44] / 0.01

= -20.24/0.01

= -2023.94

Applying h = -0.01

= [6(-2 - 0.01)² - 44] /( -0.01)

= [6(-2.01)² - 44] / (-0.01)

= [6(4.04) - 44] / (-0.01)

= 19.76/0.01

= 1976

Average = [-2023.94 + 1976)] / 2

= -47.94/2

= -23.97

Approximately -24.

b) At x = 0

f(x) = 6x² - 4

f(0) = 6(0)² - 4

= 0 - 4

= -4

[f(0 + h) - f(0)] / h = [(6(0 + h)² - 4) - (-4)] / h

= [6h² - 4 + 4] / h

= 6h² / h

= 6h

Applying h = 0.01

= 6(0.01)

= 0.06

Applying h = -0.01

= 6(-0.01)

= -0.06

Average = [0.06 + (-0.06)] / 2

= 0

c) at x = 4

f(4) = 6(4)² - 4

= 6(4) - 4

= 96 - 4

= 92

[f(4 + h) - f(4)] / h = [(6(4 + h)² - 4) - 92] / h

= [(6(16 + 8h + h²) - 4) - 92] / h

= [96 + 48h + 6h² - 4 - 92] / h

= [96 + 48h + 6h² - 96] / h

= [48h + 6h²] / h

= h(48 + 6h)/h

= 48 + 6h

Applying h = 0.01

= 48 + 6(0.01)

= 48 + 0.06

= 48.06

Applying h = -0.01

= 48 + 6(-0.01)

= 48 - 0.06

= 47.94

Average = [48.06 + 47.94] / 2

= 96/2

= 48

d) at x = 8

f(x) = 6x² - 4

f(8) = 6(8)² - 4

= 6(64) - 4

= 384 - 4

= 380

[f(8 + h) - f(8)] / h = [(6(8 + h)² - 4) - 380] / h

= [6(8 + h)² - 24 - 380] / h

= [6(8 + h)² - 404] / h

Applying h = 0.01

= [6(8 + 0.01)² - 404] / 0.01

= [6(8.01)² - 404] / 0.01

= [6(64.16) - 404] / 0.01

= [384.96 - 404] / 0.01

= [384.96 - 404] / 0.01

= -19.03/0.01

= -1903.94

Applying h = -0.01

= [6(8 - 0.01)² - 404] / (-0.01)

= [6(7.99)² - 404] / (-0.01)

= [6(63.84) - 404] / (-0.01)

= [383.04 - 404] / (-0.01)

= [384.96 - 404] / (-0.01)

= -20.95/(-0.01)

= 2095.94

Average = [-1903.94 + 2095.94] / 2

= 192/2

96

Problem 2 :

An object is sent through the air. Its height is modelled by the function

h(x) = -5x² + 3x + 65

where h(x) is the height of the object in meters and x is the time in seconds.  Estimate the instantaneous rate of change in the object’s height at 3 s.

Solution :

Write the difference quotient for the average rate of change in volume as the side length changes between 2 and any value

𐤃y/𐤃x = [f(a + h) - f(a)] / h

h(x) = -5x² + 3x + 65

f(3) = -5(3)² + 3(3) + 65

= -5(9) + 9 + 65

= -45 + 74

= 29

f(3 + h) = -5(3 + h)² + 3(3 + h) + 65

= -5(9 + 6h + h²) + 9 + 3h + 65

= -45 - 30h - 5h² + 9 + 3h + 65

= -45 - 27h - 5h² + 74

= - 27h - 5h² + 29

[f(3 + h) - f(3)] / h = [(- 51h - 5h² + 29) - 29] / h

= (-27h - 5h²) / h

= h(- 27 - 5h) / h

= (- 27 - 5h)

Applying h = 0.01

= -(27 + 5(0.01))

= - (27 + 0.05)

= -27.05

Applying h = -0.01

= -(27 + 5(-0.01))

= - (27 - 0.05)

= -26.95

Average = [-27.05 - 26.95] / 2

= 54/2

= 27 m/s

So, the required rate of change is 27 meter/second.

Your second block of text...