DETERMINING THE END BEHAVIOUR OF A RATIONAL FUNCTION

The end behavior of a rational function only describes the behavior of the function when x -> ∞ or x ->-∞.

The end behavior of a rational function y = f(x)/g(x) can have three forms.

i) Horizontal asymptote :

When the degree of f(x) is less than or equal to the degree of g(x), the rational function will have the horizontal asymptote.

ii) Oblique asymptote :

When the degree of f(x) is one more than the degree of g(x), the rational function will have oblique or slant asymptote.

iii) Asymptotic to a polynomial :

When the degree of f(x) is at least two more than the degree of g(x), the rational function will behave like a polynomial.

How to find oblique asymptote ?

The equation of the oblique asymptotes and the end behaviour polynomials are determined by dividing the polynomial f(x) by the polynomial g(x). The equation, ignoring the remainder is the equation for the enbd behaviour model.

How to check if the asymptote touches or crosses the function ?

The process of judging whether the function touches or crosses its asymptotes involves solving the system of equation that consists of the equation of the end behaviour and the rational function.

When the system results in a null solution, such as 12 = 5, the graph never touch.

When the system has solution, such as x = 1.5, the x-value provides the x-coordinate of the point of intersection.

Problem 1 :

Determine the horizontal asymptote of

by evaluating the limit as x approaches ± infinity. Does the function intersect its horizontal asymptote ?

Solution :

Highest exponent of the numerator = 1

Highest exponent of the denominator = 1

Exponent of the numerator = exponent of the denominator

Horizontal asymptote y = Coefficient of x in the numerator / coefficient of x in the denominator

= 2/1

y = 2

Check if the asymptote intersects y = 2 :

(2x - 4)/(x + 3) = 2

2x - 4 = 2(x + 3)

2x - 4 = 2x + 6

It does not have solution. Then, no solution.

Conclusion :

The graph does not intersect its horizontal asymptote.

Problem 2 :

Determine the horizontal asymptote

by evaluating the limit as x approaches ± infinity. Does the function intersect its horizontal asymptote ?

Solution :

Highest exponent of the numerator = 1

Highest exponent of the denominator = 2

Exponent of the numerator < exponent of the denominator

Horizontal asymptote y = 0

Check if the horizontal asymptote intersects at y = 0 :

At x = 2, the curve is intersecting the horizontal asymptote.

Conclusion :

It has horizontal asymptote at y = 0
The horizontal asymptote is intersecting the curve at (2, 0).

Problem 3 :

Determine the horizontal asymptote

by evaluating the limit as x approaches ± infinity. Does the function intersect its horizontal asymptote ?

Solution :

Highest exponent of the numerator = 2

Highest exponent of the denominator = 2

Exponent of the numerator = exponent of the denominator

Horizontal asymptote y = Coefficient of x in the numerator / coefficient of x in the denominator

= 1/1

y = 1

Check if the horizontal asymptote intersects at y = 1 :

Conclusion :

It has horizontal asymptote at y = 1
The horizontal asymptote is intersecting the curve at (4, 1).

Problem 4 :

The rational function,

has an oblique asymptote. Use long division to divide the numerator by the denominator. The line y = quotient, is the oblique asymptote.

Solution :

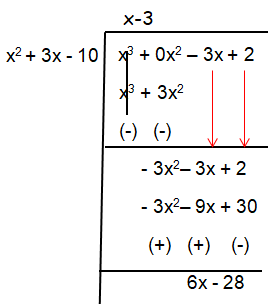
y = x - 3 is the oblique asymptote.

Check if the oblique asymptote intersects the the curve :

Applying x = 1.75 in y = x - 3

y = 1.75 - 3

y = -1.25

Conclusion :

It has horizontal asymptote at y = x - 3
The horizontal asymptote is intersecting the curve at (1.75, -1.25).

DETERMINING THE END BEHAVIOUR OF A RATIONAL FUNCTION

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling