FINDING THE COORDINATES FOR THE GIVEN TRANSLATION

Moving a coordinate from one place to another place with horizontal or vertical movement is called translation.

Always points will be in the form of (x, y).

• Moving the point towards right, x will become x + h
• Moving the point towards left, x will become x - h
  
• Moving the point towards up, then y will become y + k
  
• Moving the point towards down,  y will become y - k

Problem 1 :

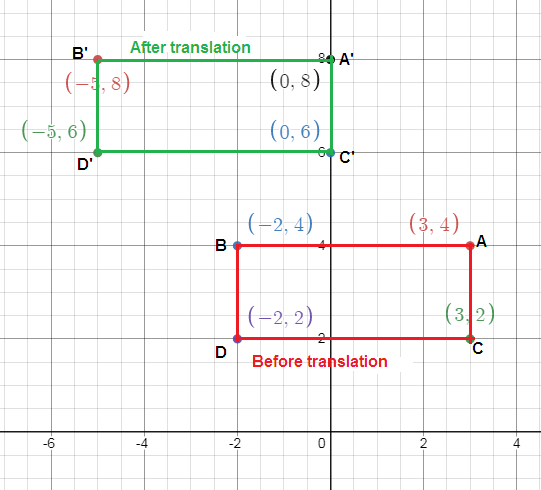
After moving a picnic table at a shelter, the coordinates of its corners are (3, 4), (-2, 4), (3, 2) and (-2, 2). If the picnic table was moved 3 units left and 4 units up, what were the original coordinates of the picnic table?

Solution:

Original coordinates 

Let A(3, 4), B(-2, 4), C(3, 2) and D(-2, 2).

We have to do a translation to the left by 3 units and up by 4 units.

h = -3 and k = 4

A(3, 4) ---> (3 - 3, 4 + 4) ---> A'(0, 8)

B(-2, 4) ---> (-2 - 3, 4 + 4) ---> B'(-5, 8)

C(3, 2) ---> (3 - 3, 2 + 4) ---> C'(0, 6)

D(-2, 2) ---> (-2 - 3, 2 + 4) ---> D'(-5, 6)

Problem 2 :

The Larsons' tent corners have the coordinates (0, 5), (5, 5), (5, 0), (0, 0). They want to move it 5 units right and 2 units up. What are the new coordinates of the tent corners?

Solution:

Let A(0, 5), B(5, 5), C(5, 0) and D(0, 0).

We have to do a translation to the right by 5 units and up by 2 units.

So, the vertices of image should be added with 5 units and add 2 units up to get the vertices of pre image.

A(0, 5) ---> (0 + 5, 5 + 2) ---> A'(5, 7)

B(5, 5) ---> (5 + 5, 5 + 2) ---> B'(10, 7)

C(5, 0) ---> (5 + 5, 0 + 2) ---> C'(10, 2)

D(0, 0) ---> (0 + 5, 0 + 2) ---> D'(5, 2)

Problem 3 :

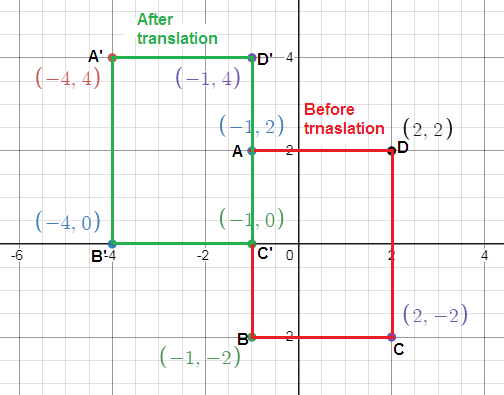
Jeanne's flower bed has the following coordinates for its corners: (-1, 2), (-1, -2), (2, -2), (2, 2). She wants to move it 3 units left and 2 units up. What are the coordinates of the corners of the new flower bed?

Solution:

Let A(-1, 2), B(-1, -2), C(2, -2) and D(2, 2).

We have to do a translation to the left by 3 units and up by 2 units.

So, the vertices of image should be subtracted with 3 units and add 2 units up to get the vertices of pre image.

A(-1, 2) ---> (-1 - 3, 2 + 2) ---> A'(-4, 4)

B(-1, -2) ---> (-1 - 3, -2 + 2) ---> B'(-4, 0)

C(2, -2) ---> (2 - 3, -2 + 2) ---> C'(-1, 0)

D(2, 2) ---> (2 - 3, 2 + 2) ---> D'(-1, 4)

Problem 4 :

The corners of home plate are now at (0, 0), (1, 0), (1, 1) and (0, 1). It was moved 2 units right and 3 units down from its previous position. What are the original coordinates of home plate?

Solution:

Let A(0, 0), B(1, 0), C(1, 1) and D(0, 1).

We have to do a translation to the right by 2 units and down by 3 units.

So, the vertices of image should be added with 2 units and subtracted with 3 units to get the vertices of pre image.

A(0, 0) ---> (0 + 2, 0 - 3) ---> A'(2, -3)

B(1, 0) ---> (1 + 2, 0 - 3) ---> B'(3, -3)

C(1, 1) ---> (1 + 2, 1 - 3) ---> C'(3, -2)

D(0, 1) ---> (0 + 2, 1 - 3) ---> D'(2, -2)

Problem 5 :

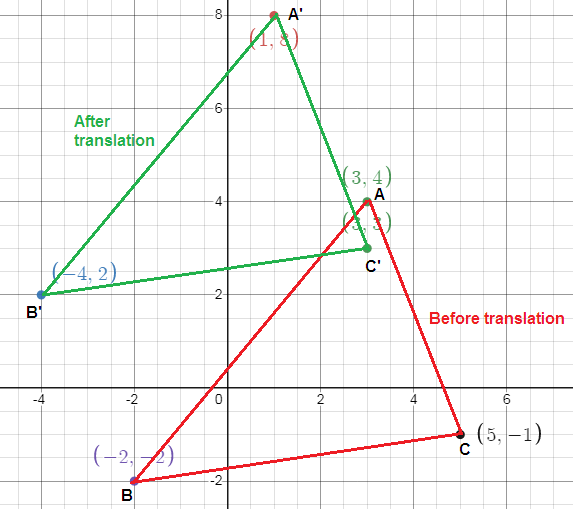
A company is designing a logo that uses a triangle. The triangle's corners has coordinates (3, 4), (-2, -2) and (5, -1). They decide to move the triangle left 2 units and up 4 units. What are the new coordinates of the corners of the translated triangle?

Solution:

Let A(3, 4), B(-2, -2) and C(5, -1).

We have to do a translation to the left by 2 units and up by 4 units.

So, the vertices of image should be subtracted with 2 units and added with 2 units to get the vertices of pre image.

A(3, 4) ---> (3 - 2, 4 + 4) ---> A'(1, 8)

B(-2, -2) ---> (-2 - 2, -2 + 4) ---> B'(-4, 2)

C(5, -1) ---> (5 - 2, -1 + 4) ---> C'(3, 3)

Problem 6 :

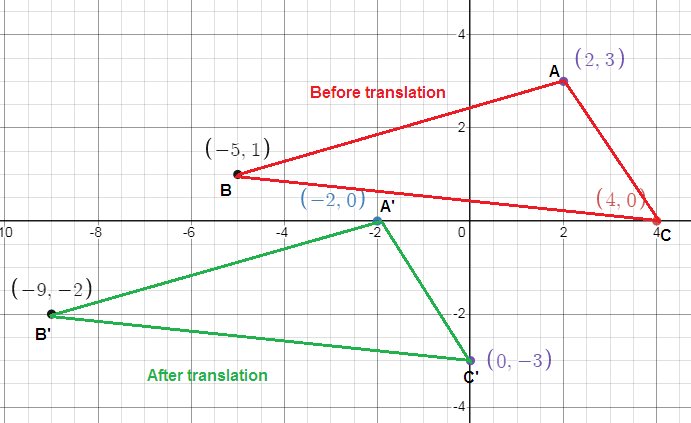
The final position of a T-shirt design has corners at (2, 3), (-5, 1) and (4, 0). This is a translation of 4 units left and 3 units down from the original position. What were the coordinates of the original corners?

Solution:

Let A(2, 3), B(-5, 1) and C(4, 0).

We have to do a translation to the left by 4 units and down by 3 units.

So, the vertices of image should be subtracted with 4 units and subtract 3 units to get the vertices of pre image.

A(2, 3) ---> (2 - 4, 3 - 3) ---> A'(-2, 0)

B(-5, 1) ---> (-5 - 4, 1 - 3) ---> B'(-9, -2)

C(4, 0) ---> (4 - 4, 0 - 3) ---> C'(0, -3)