DETERMINE WHICH GRAPH REPRESENTS POLYNOMIAL FUNCTION

The domain of a polynomial function is the set of real numbers, x ∈ R

• The range of a polynomial function may be all real numbers, or it may have a lower bound or an upper bound (but not both).
• The graphs of polynomial functions do not have horizontal or vertical asymptotes.
• The graphs of polynomial functions of degree zero are horizontal lines. The shape of other graphs depends on the degree of the function. Five typical shapes are shown for various degrees:

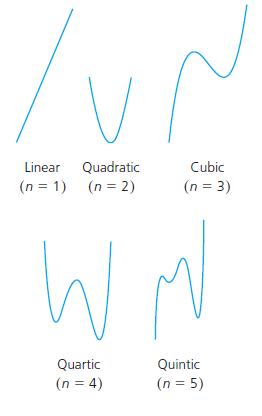
Determine which graphs represent polynomial functions. Explain how you know.

Problem 1 :

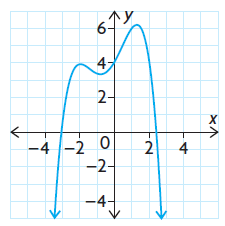
Solution :

This represents a polynomial function because the domain is the set of all real numbers, the range does not have a lower bound, and the graph does not have horizontal or vertical asymptotes. 

Problem 2 :

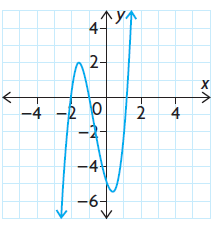
Solution :

This represents a polynomial function because the domain is the set of all real numbers, the range is the set of all real numbers, and the graph does not have horizontal or vertical asymptotes. 

Problem 3 :

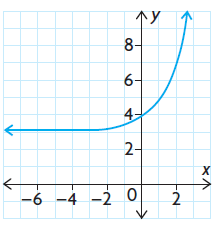
Solution :

This is not a polynomial function because it has a horizontal asymptote.

Problem 4 :

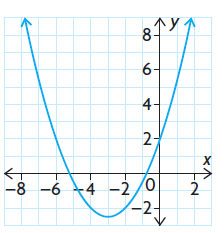
Solution :

This represents a polynomial function because the domain is the set of all real numbers, the range does not have an upper bound, and the graph does not have horizontal or vertical asymptotes

Problem 5 :

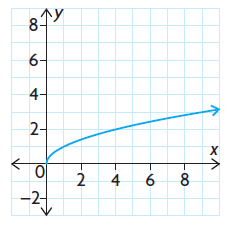
Solution :

This is not a polynomial function because its domain is not all real numbers

Problem 6 :

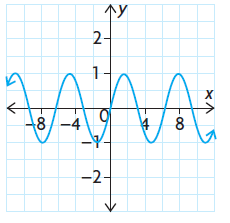
Solution :

This is not a polynomial function because it is a periodic function

Problem 7 :

Determine the equation of the polynomial function from graph.

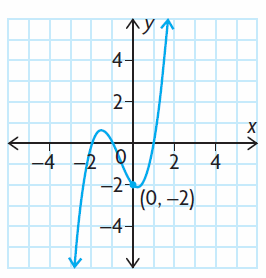
Solution :

By observing the graph, it is clear that the required polynomial will be cubic.

The x-intercepts are -2, -1 and 1.

Factored form are (x + 2)(x + 1)(x - 1)

The required polynomial will be in the form,

y = a(x + 2)(x + 1)(x - 1)

y-intercept = - 2

-2 = a(0 + 2)(0 + 1)(0 - 1)

-2 = -2a

a = 1

By applying the value of a, we get

y = (x + 2)(x + 1)(x - 1)

= (x + 2)(x² - 1²)

= x³ - x + 2x² - 2

= x³ + 2x² - x - 2

Problem 8 :

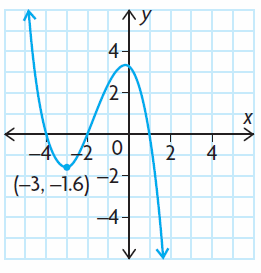
Determine the equation of the polynomial function from graph.

Solution :

By observing the graph, it is clear that the required polynomial will be cubic.

The x-intercepts are -4, -2 and 1.

Factored form are (x + 4)(x + 2)(x - 1)

The required polynomial will be in the form,

y = a(x + 4)(x + 2)(x - 1)

The curve passes through the point (-3, -1.6)

-1.6 = a(-3 + 4)(-3 + 2)(-3 - 1)

-1.6 = a(1)(-1)(-4)

1.6 = -4a

a = -1.6/4

a = -0.4

By applying the value of a, we get

y = (-2/5) (x + 4)(x + 2)(x - 1)

Problem 9 :

Determine the quadratic function that has zeros at -3 and -5 if f(7) = -720

Solution :

The required quadratic polynomial will be in the form of

f(x) = a(x - p) (x - q)

Since the zeroes are -3 and -5, we may write it the factored form.

(x + 5)(x + 3) are the factors.

f(x) = a(x + 5)(x + 3)

Applying x = 7 and y = -720, we get

-720 = a(7 + 5)(7 + 3)

-720 = a(12) (10)

120a = -720

a = -720/120

a = -6

applying the value of a, we get the polynomial.

f(x) = -6(x + 5)(x + 3)

Problem 10 :

Determine the cubic function that has zeros at -2, 3 and 4 if f(5) = 28

Solution :

Zeroes of the cubic function is,

x = -2, x = 3 and x = 4

The factors are (x + 2)(x - 3)(x - 4)

f(x) = a(x + 2)(x - 3)(x - 4)

Applying x = 5 and y = 28 from f(5) = 28, we get

28 = a(5 + 2)(5 - 3)(5 - 4)

28 = a(7)(2)(1)

14a = 28

a = 28/14

a = 2

Applying the value of a, we get

f(x) = 2(x + 2)(x - 3)(x - 4)

Problem 11 :

The function has a zero when x = 2

f(x) = kx³ - 8x² - x + 3k + 1

Determine the value of k. Graph f(x) and determine all the zeros. Then rewrite f(x) in factored form.

Solution :

f(x) = kx³ - 8x² - x + 3k + 1

The function has the zero when x = 2, so f(2) = 0

0 = k(2)³ - 8(2)² - 2 + 3k + 1

0 = 8k - 8(4) - 2 + 3k + 1

0 = 8k - 32 - 2 + 3k + 1

0 = 11k - 33

11k = 33

k = 33/11

k = 3

So, the required value of k is 3.

f(x) = 3x³ - 8x² - x + 3(3) + 1

= 3x³ - 8x² - x + 9 + 1

= 3x³ - 8x² - x + 10

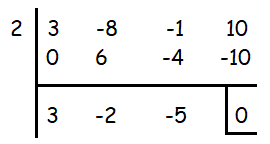
= (x - 2) (3x² - 2x - 5)

= (x - 2) (3x² - 5x + 3x - 5)

= (x - 2) (3x² - 5x + 3x - 5)

= (x - 2)(x + 1) (3x - 5)

So, the required factored form is f(x) = (x - 2)(x + 1) (3x - 5)