DETERMINE WHETHER THE GIVEN PAIR OF FIGURES ARE SIMILAR OR NOT

Problem 1 :

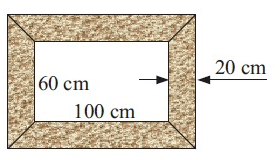
A 20 cm wide picture frame surrounds a painting which is 100 cm by 60 cm. Are the two rectangles shown here similar?

Solution :

Picture frame = 20 cm

Surrounds a painting = 100 cm by 60 cm

100 : 60 = 5 : 3

Inside rectangle has sides in 5 : 3

100 + 60 = 160

20 cm wide picture frame = 160 – 20

= 140

140 : 100 = 7 : 5

Outside rectangle has sides in 7 : 5

And 5 : 3 ≠ 7 : 5

Therefore it is not similar.

Give brief reasons why these figures possess similar triangles:

Problem 2 :

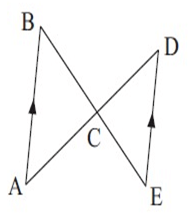
Solution :

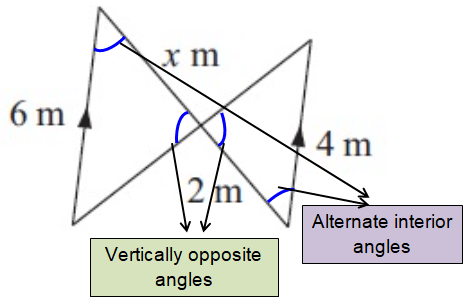
 ∠ABE =  ∠DEB  (Alternate interior angles)

 ∠ACB =  ∠DCE  (Vertically opposite angles)

So, triangles are equiangular and therefore, similar.

Problem 3 :

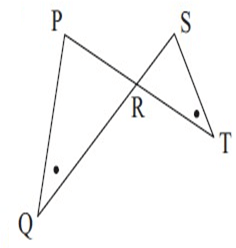
Solution :

∠PQR =  ∠STR (given)

∠PQT = ∠STP (Alternate interior angles)

∠PRQ = ∠SRT (Vertically opposite angles)

So, triangles are equiangular and therefore, similar.

Problem 4 :

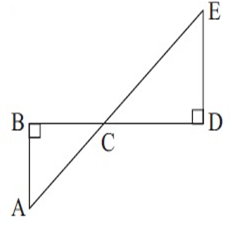
Solution :

Both triangles are right angled.

∠BAE = ∠EDA (Alternate interior angles)

∠BCA = ∠DCE (Vertically opposite angles)

So, triangles are equiangular and therefore similar.

Problem 5 :

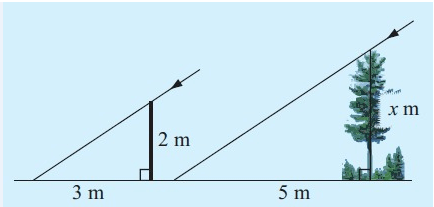
At 4 pm one day the shadow of a pine tree was 5 m long. At the same time a 2 m long broom handle had a shadow which was 3 m long. How high is the pine tree?

Solution :

The shadow of a pine tree = 5 m long

The same time = 2 m long

Broom handle had a shadow = 3 m long

2/3 = x/5

10 = 3x

x = 3.3

So, the pine tree high is 3.3 m.

After establishing similarity, find the unknowns in:

Problem 6 :

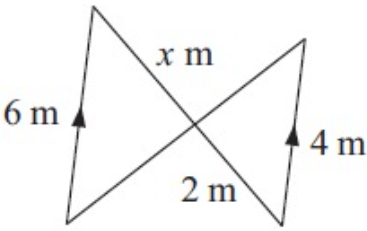
Solution :

6/4 = x/2

3/2 = x/2

x = 3

Problem 7 :

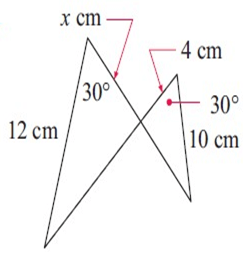
Solution :

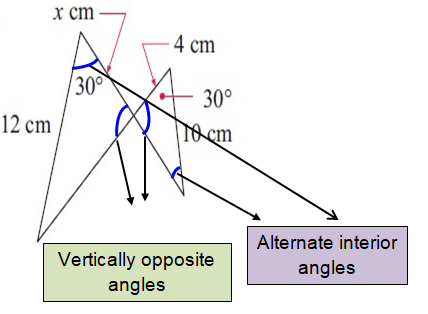
12/10 = x/4

6/5 = x/4

x = 4.8

Problem 8 :

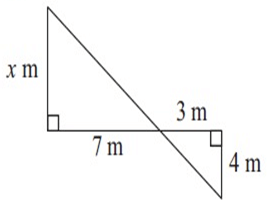
Solution :

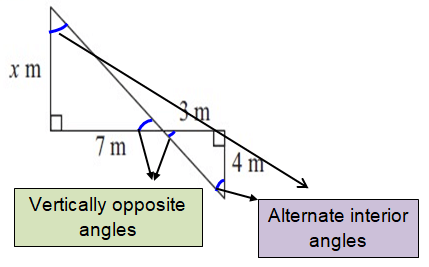
x/4 = 7/3

3x = 28

x = 9 1/3 

Problem 9 :

The Mexican flag is 63 inches long and 36 inches high. Is the drawing at below similar to the Mexican flag ?

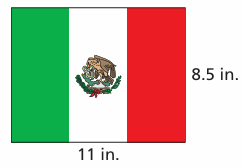
Solution :

Length of the original flag = 63 inches

Length of flag shown = 11 inches

Width of original flag = 36 inches

Width of flag shown = 8.5 inches

63/11 = 36/8.5

5.72 not equal to 4.23

So, the flag show above is not similar to the original flag.

Problem 10 :

A student’s rectangular desk is 30 inches long and 18 inches wide. The teacher’s rectangular desk is 60 inches long and 36 inches wide. Are the desks similar?

Solution :

Length of student's rectangular desk = 30 inches

Width = 18 inches

Length of teacher's rectangular desk = 60 inches

Width = 36 inches

30 : 60 = 18 : 36

1 : 2 = 1 : 2

Since the corresponding sides are in the same ratio, the desks are similar.

Problem 11 :

The two triangles are similar. Find the measure of the angle

a) ∠B      b)  ∠L   c)  ∠J

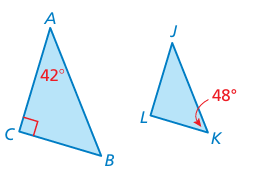
Solution :

a) 

In triangle ABC,

∠A + ∠B + ∠C = 180

42 + ∠B + 90 = 180

132 + ∠B = 180

∠B = 180 - 132

∠B = 48

b)  ∠L = 90

c)  ∠J = 42

Problem 12 :

Given △FGH ∼ △QRT, name the corresponding angles and the corresponding sides.

Solution :

∠F = ∠Q

∠G = ∠R

∠H = ∠T

Corresponding sides are,

FG and QR

GH and RT

FH and QT

Problem 13 :

You want to buy only photos that are similar rectangles. Which of the photo sizes should you buy ?

4 in × 5 in

5 in × 7 in

8 in × 12 in

11 in × 14 in

18 in × 27 in

Solution :

Comparing the corresponding lengths and widths, we get

8 : 18 = 12 : 27

8/18 = 12/27

4/9 = 4/9

So, we may purchase the photos which has the measure of 8 in × 12 in and 18 in × 27 in.

Problem 14 :

Are the following figures always, sometimes, or never similar? Explain.

a. Two triangles

b. Two squares

c. Two rectangles

d. A square and a triangle

Solution :

a. Two triangles will be similar sometimes

b. All squares have four 90° angles, and since all four sides of a square are equal, any two squares will have sides that are proportional. This makes them always the same shape.

c. While all rectangles have four 90° angles, their sides are not necessarily proportional. So, rectangles will be similar sometimes.

d. A square and a triangle will never be similar.

Problem 15 :

Can you draw two quadrilaterals each having two 130° angles and two 50° angles that are not similar? Justify your answer.

Solution :

Yes, the two quadrilaterals may be one isosceles trapezium and another parallelogram. So, they may not be similar.

Problem 16 :

All of the angle measures in the sign are 90°.

a. Each side length is increased by 20%. Is the new sign similar to the original?

b. Each side length is increased by 6 inches. Is the new sign similar to the original?

Solution :

a) Let the length of the rectangle be x, by increasing 20% of length we get 120% of x

Let width of the rectangle be y, increasing 20% the new width 120% of y

x : 120% x = y : 120% of y

x : 1.20x = y : 1.20y

So, they are similar.

b) After increasing 6 inches, then new length will be x + 6

x : y = (x + 6) : y

So, they are not similar.