DETERMINE WHETHER EACH SET OF ORDERED PAIRS IS A FUNCTION OR NOT

Which of the following set of ordered pairs are functions ? Give reasons.

Problem 1 :

{(1, 3), (2, 4), (3, 5), (4, 6)}

Solution :

Given, {(1, 3), (2, 4), (3, 5), (4, 6)}

Let X be the set of inputs and Y be the set of outputs.

Inputs (X) = {1, 2, 3, 4}

Outputs (Y) = {3, 4, 5, 6}

Create a mapping of the following relation,

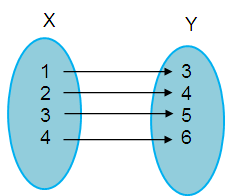
Form the arrow diagram, we understand that each x – value is being paired with only one y – value. So, this set of ordered pairs represents a function.

Problem 2 :

{(1, 3), (3, 2), (1, 7), (-1, 4)}

Solution :

Given, {(1, 3), (3, 2), (1, 7), (-1, 4)}

Let X be the set of inputs and Y be the set of outputs.

Inputs (X) = {1, 3, 1, -1}

Outputs (Y) = {3, 2, 7, 4}

Create a mapping of the following relation,

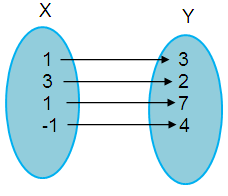
Form the arrow diagram, we understand that each x – value is being paired with only one y – value. So, this set of ordered pair represents a functions.

Problem 3 :

{(2, -1), (2, 0), (2, 3), (2, 11)}

Solution :

Given, {(2, -1), (2, 0), (2, 3), (2, 11)}

Let X be the set of inputs and Y be the set of outputs.

Inputs (X) = {2}

Outputs (Y) = {-1, 0, 3, 11}

Create a mapping of the following relation,   

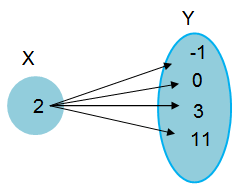
The input 2 has associate with more than one output .

So, this set of ordered pairs dose not represent a function.

Problem 4 :

{(7, 6), (5, 6), (3, 6), (-4, 6)}

Solution :

Given, {(7, 6), (5, 6), (3, 6), (-4, 6)}

Let X be the set of inputs and Y be the set of outputs.

Inputs (X) = {7, 5, 3, -4}

Outputs (Y) = {6, 6, 6, 6}

Create a mapping of the following relation,

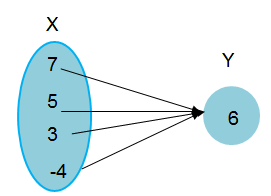
Every input is having output, no input is having more than one output. So, this set of ordered pairs represent a function.

Problem 5 :

{(0, 0), (1, 0), (3, 0), (5, 0)}

Solution :

Given, {(0, 0), (1, 0), (3, 0), (5, 0)}

Let X be the set of inputs and Y be the set of outputs.

Inputs (X) = {0, 1, 3, 5}

Outputs (Y) = {0, 0, 0, 0}

Create a mapping of the following relation,

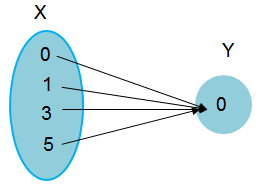
Each input is associated with outputs. No input is having more than one out put. So, it is a function.

Problem 6 :

{(0, 0), (0, -2), (0, 2), (0, 4)}

Solution :

Given, {(0, 0), (0, -2), (0, 2), (2, 11)}

Let X be the set of inputs and Y be the set of outputs.

Inputs (X) = {0}

Outputs (Y) = {0, -2, 2, 4}

Create a mapping of the following relation,

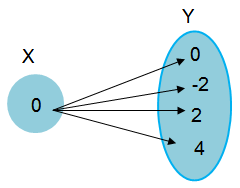
Input 0 is having more than one output. So, this set of ordered pair doesn't represent a function.