DETERMINE WHETHER A FUNCTION HAS AN INVERSE

Which of the following functions have inverses ? If each of these cases, write down the inverse function.

Problem 1 :

{ (1, 2) (2, 4) (3, 5) }

Solution :

Every element is associated with different different outputs. So, it is a one to one function. It has inverse.

Inverse function :

{ (2, 1) (4, 2) (5, 3) }

Problem 2 :

{ (-1, 3) (0, 2) (1, 3) }

Solution :

The given relation is a function, but it is not one to one.

Because two different inputs -1 and 1 is having the output 3. So, it is not one to one, then inverse function does not exists.

Problem 3 :

{ (2, 1) (-1, 0) (0, 2) (1, 3) }

Solution :

Converting into arrow diagram,

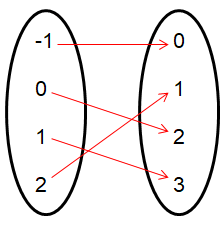
it is clear that the given relation is one to one. So, it has inverse.

Inverse function :

{ (1, 2) (0, -1) (2, 0) (3, 1 ) }

Problem 4 :

{ (-1, -1) (0, 0) (1, 1) }

Solution :

Converting into arrow diagram,

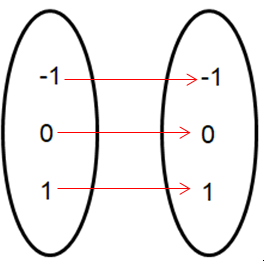
it is clear that the given relation is one to one. So, it has inverse.

Inverse function :

{ (-1, -1) (0, 0) (1, 1) }

Which of the following function has inverse function.

Problem 5 :

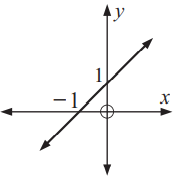
Solution :

When we draw the horizontal line, it will intersect the graph at one point. So, it is one to one function and it has inverse.

Problem 6 :

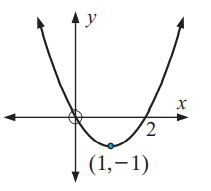
Solution :

When we draw the horizontal line, it doesn't intersect the graph at one point. So, it is not one to one function and it doesn't have inverse.

Problem 7 :

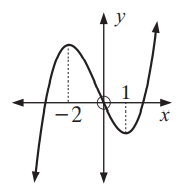
Solution :

When we draw the horizontal line, it doesn't intersect the graph at one point. So, it is not one to one function and it doesn't have inverse.

For each of the following graphs determine :

i) range and domain

ii)  find x and y intercepts

iii)  Whether it is a function

iv)  if it has a inverse function

Problem 8 :

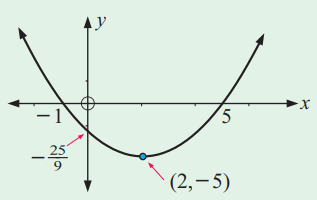
i)  Domain : (-∞,∞) and Range [-2, ∞)

ii) x-intercepts are -1 and 5, y-intercept is -25/9

iii) The vertical line will intersect the curve at most one point. So, it is a fucntion.

iv) The horizontal line will intersect the graph at two points(More than one point). Not one to one. Doesn't have inverse function.

Problem 9 :

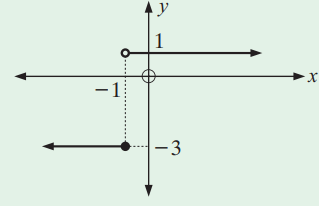
i)  Domain : (-∞,∞) and Range [-3, 1)

ii) There is no x and y-intercepts.

iii) The vertical line will intersect the curve at most one point. So, it is a function.

iv) The horizontal line will intersect the graph at two points(More than one point). Not one to one. Doesn't have inverse function.