DETERMINE THE NUMBER OF SOLUTIONS TO A SYSTEM OF EQUATIONS

A set of equations with two variables is called system of linear equations.

A system of linear equations can have 

(i)  No solution (Parallel lines)

(ii)  Infinitely many solutions (Coinciding lines)

(iii)  Unique solution (Intersecting lines)

What is solution ?

The point of intersection is known as solution.

No solution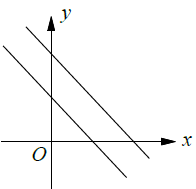

Infinitely Many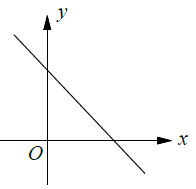

Intersecting lines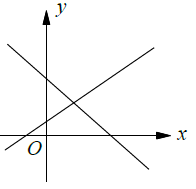

Parallel will have same slope and different y-intercepts Coinciding lines will have same slope and same y intercept. Intersecting lines will at one point.

Problem 1 :

x - 3y = 4

2(x - 1) - 6(y + 2) = -6

How many solutions (x, y) are there to the system of equations above ?

(a)  zero      (b)  One    (c)  Two     (d)  More than two

Solution :

x - 3y = 4 -----(1)

2(x - 1) - 6(y + 2) = -6 -----(2)

From (2)

2x - 2 - 6y - 12 = -6

2x - 6y = -6 + 12 + 2

2x - 6y = 8

Dividing by 2, we get

x - 3y = 4

Since both are same lines, they will be coinciding lines and it has infinitely many solutions.

Problem 2 :

ax + 4y = 14

5x + 7y = 8

In the system of equations above, a is constant and x and y are variables, If the system has no solution, what is the value of a ?

(a)  20/7      (b)  35/4    (c)  -35/4    (d)  -20/7

Solution :

ax + 4y = 14

5x + 7y = 18

Since it has no solution, they are parallel lines. So,

m₁ = m₂

(1) = (2)

 -a/4 = -5/7

a = 20/7

Problem 3 :

ax + (1/2)y = 16

4x + 3y = 8

In the system of equations above, a is constant. If the system has no solution, what is the value of a ?

Solution :

ax + (1/2)y = 16

4x + 3y = 8

It has no solutions, they must be parallel and they will have same slopes.

(1) = (2)

-2a = -4/3

a = 2/3

Problem 4 :

Paper West has produced 5000 kg of napkins. It continues to manufacture 350 kg of napkins per week. Northern Paper manufactures napkins at a rate of 1400 kg per month and has already produced 28000 kg. Assume one month has exactly four weeks.

a) Write a system of linear equations to represent the manufacturing of the napkins.

b) Explain how the number of solutions to the system relates to this situation.

Solution :

Let x be the number of weeks and y be the quantity of napkins produced.

a)

Paper west manufactures :

y = 5000 + 350x

Northern paper manufactures :

= 1400/ 4

= 350 kg per week

y = 28000 + 350x

b) The system will have unique solution. When the companies manufacturing in the same rate, at which month both companies will produce the same number of napkins.

Problem 5 :

For the linear system 2x + 3y = 12 and 4x + 6y = C, what value(s) of C will give the system

a) an infinite number of solutions?

b) no solution?

Solution :

2x + 3y = 12 ----(1)

4x + 6y = C ------(2)

From (1), 3y = -2x + 12

y = (-2/3)x + 12/3

y = (-2/3)x + 4

From (2), 6y = -4x + C

y = (-4x/6) + C/6

y = (-2x/3) + C/6

a) When the system of linear equations has infinite number of solutions, then

m₁/m₂ = c₁/c₂

-2/3 / (-2/3) = 4/(C/6)

1 = 24/C

C = 24

b) No solution

m₁/m₂ ≠ c₁/c₂

-2/3 / (-2/3) ≠ 4/(C/6)

1 ≠ 24/C

C ≠ 24

Problem 6 :

Without graphing, decide whether the system of equations has one solution, no solution, or infinitely many solutions.

y = 3x + 14

y = –3x + 14

Solution :

y = 3x + 14

Slope = 3 and y-intercept = 14

y = -3x + 14

Slope = -3 and y-intercept = 14

By observing the above, the slopes are not equal. So, the system has unique solution.

Problem 7 :

Without graphing the equations, decide whether the system has one solution, no solution, or infinitely many solutions.

5y = x – 9

4x – 10y = 18

Solution :

Finding slope and y-intercept of these two lines :

From (1), 5y = x – 9

y = (1/5) x - (9/5)

4x – 10y = 18

10y = 4x - 18

y = 4x/10 - (18/10)

y = 2x/5 - 9/5

From (2), 4x – 10y = 18

10y = 4x - 18

y = 4x/10 - (18/10)

y = 2x/5 - 9/5

By observing slope and y-intercepts, slopes are equal and y-intercepts are also equal. Then the system has infinite number of solutions.