DETERMINE THE ELEMENTS OF GIVEN SETS FROM VENN DIAGRAM

Operations involving set theory :

(i) Union

The union of two sets A and B is the set of all those elements which are either in A or in B, i.e. A ∪ B

(ii) Intersection

The intersection of two sets A and B is the set of all elements which are common. The intersection of these two sets is denoted by A ∩ B.

(iii) Difference

The set which contains the elements which are either in set A or in set B but not in both is called the difference between two given sets.

(iv) Complementation

In set theory, the complement of a set A, often denoted by Ac (or A′), are the elements not in A. A circle filled with red inside a square.

Problem 1 :

Find the following in the venn diagram.

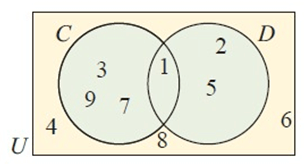
a) List :

i) set C

ii) set D

iii) set U

iv) set C ∩ D

v) set C ∪ D

b) Find :

i) n(C)

ii) n(D)

iii) n(U)

iv) n(C ∩ D)

v) n(C ∪ D)

Solution :

i) set C = {1, 3, 7, 9}

ii) set D = {1, 2, 5}

iii) set U = {1, 2, 3, 4, 5, 6, 7, 8, 9}

iv) set C ∩ D = {1}

v) set C ∪ D = {1, 2, 3, 5, 7, 9}

b) 

i) n(C) = 4

ii) n(D) = 3

iii) n(U) = 9

iv) n(C ∩ D) = 1

v) n(C ∪ D)

n(C ∪ D) = n(C) + n(D) – n(C ∩ D)

= 4 + 3 – 1

= 6

Problem 2 :

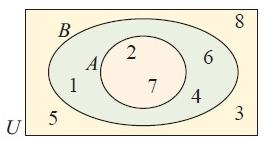
Find the following.

i) set A

ii) set B

iii) set U 

iv) set A ∩ B 

v) set A ∪ B

i) n(A)

ii) n(B)

iii) n(U)

iv) n(A ∩ B)

v) n(A ∪ B)

Solution :

i) set A = {2, 7}

ii) set B = {1, 4, 6}

iii) set U = {1, 2, 3, 4, 5, 6, 7, 8}

iv) set A ∩ B = { }

v) set A ∪ B = {1, 2, 4, 6, 7}

b Find :

i) n(A) = 2

ii) n(B) = 3

iii) n(U) = 8

iv) n(A ∩ B) = { }

v) n(A ∪ B)

n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

= 2 + 3 – {}

= 5

Problem 3 :

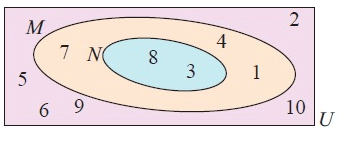
a) List the elements of :

i) U       ii) N         iii) M

b) What are n(N) and n(M)?

c) Is M  ⊆ N?

Solution :

i) U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

ii) N = {8, 3}

iii) M = {1, 4, 7}

b) n(N) = 2 and n(M) = 3

c) M ⊆ N = {1, 3, 4, 7, 8}

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More