DETERMINE THE AMPLITUDE AND PERIOD OF THE FUNCTION SHOWN IN THIS GRAPH

What is periodic ?

A function is periodic if it has a pattern of y-values that repeats at regular intervals.

What is cycle ?

One complete pattern is called cycle. A cycle may begin at any point on the graph.

What is period ?

The horizontal length of one cycle is called period of the function.

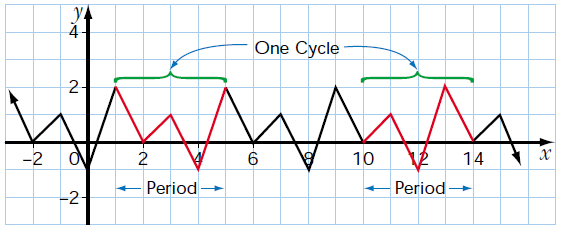
Amplitude :

Amplitude is half the difference between the maximum value (peak) and the minimum value (trough) in a cycle.

y = (Max + Min)/2

Determine whether the graph represents a periodic function. If so, identify the period and amplitude.

Problem 1 :

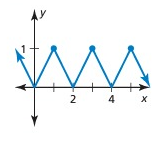
Solution:

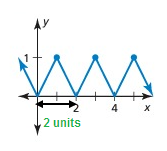
It has a pattern, so it is a periodic function.

The horizontal length of the pattern is 2 units.

So, period is 2.

Amplitude = (max - min)/2

= (1 - 0)/2

= 1/2

= 0.5

Problem 2 :

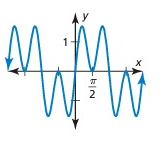
Solution:

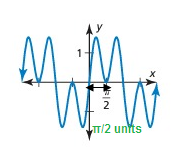
It has a pattern, so it is a periodic function.

The horizontal length of the pattern is π/2.

So, period is π/2.

Amplitude = (max - min)/2

= (1.5 - (-1.5))/2

= (1.5+1.5)/2

= 3/2

= 1.5

Problem 3 :

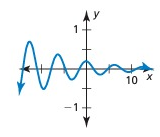
Solution :

The graph doesn't have pattern. So, it is not a periodic function.

Problem 4 :

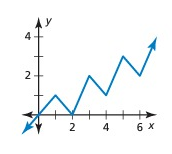
Solution:

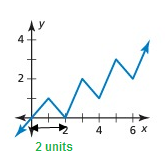
It has a pattern, but y-values is not repeating for each cycle. So, it is not a periodic function.

Identify the amplitude and period of the graph of the function.

Problem 5 :

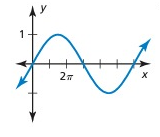
Solution:

The horizontal length of one pattern = 3π.

So, the period = 3π.

Maximum = 1, minimum = -1

 Amplitude = (Max - Min)/2

= (1 - (-1))/2

= (1 + 1)/2

= 2/2

= 1

So, amplitude = 1

Problem 6 :

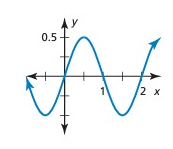
Solution:

The horizontal length of one pattern = 1

So, the period = 1

Maximum = 0.5, minimum = -0.5

 Amplitude = (Max - Min)/2

= (0.5 - (-0.5))/2

= (0.5 + 0.5)/2

= 1/2

= 0.5

So, amplitude = 0.5

Problem 7 :

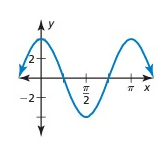
Solution:

The horizontal length of one pattern = π

So, the period = π

Maximum = 4, minimum = -4

 Amplitude = (Max - Min)/2

= (4 - (-4))/2

= (4 + 4)/2

= 8/2

= 4

So, amplitude = 4

Problem 8 :

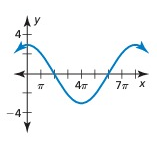
Solution:

The horizontal length of one pattern = 8π

So, the period = 8π

Maximum = 3, minimum = -3

 Amplitude = (Max - Min)/2

= (3 - (-3))/2

= (3 + 3)/2

= 6/2

= 3

So, amplitude = 3