DETERMINE IF THREE SIDES FORM A RIGHT TRIANGLE

By using Pythagorean theorem, we can determine whether the three sides will create a right triangle.

a² = b² + c²

Here the longest side can be considered as hypotenuse. We have to check, if the square of the longest side is equal to the some of squares of the remaining sides.

• If it is true, then we can decide the given sides will be sides of right triangle.
• If it is not true, then we can decide the given sides will not create right triangle.

The following figures are not drawn to scale. Which of the triangles are right angled?

Problem 1 :

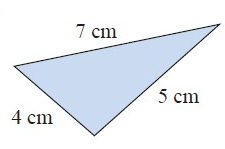
Solution :

Using Pythagorean theorem.

 7² = 4² + 5²

49 = 16 + 25

49 ≠ 41

So, it is not a right triangle.

The following figures are not drawn to scale. Which of the triangles are right angled?

Problem 2 :

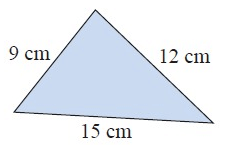
Solution :

The measure of longest side = 15

a = 15, b = 12 and c = 9

Using Pythagorean theorem.

15² = 12² + 9²

225 = 144 + 81

225 = 225

So, it is a right triangle.

Problem 3 :

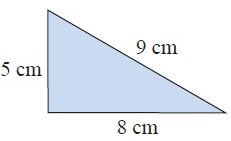
Solution :

The measure of longest side = 9 cm

a = 9, b = 8 and c = 5

Using Pythagorean theorem.

9² = 8² + 5²

81 = 64 + 25

81 ≠ 89

So, it is not a right triangle.

Problem 4 :

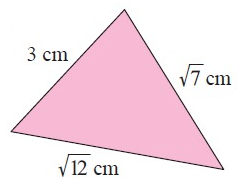
Solution :

The measure of longest side = √12

a = √12, b = √7 and c = 3

Using Pythagorean theorem.

(√12)² = (√7)² + 3²

12 = 7 + 9

12 ≠ 16

So, it is not a right triangle.

Problem 5 :

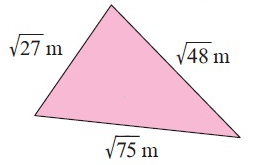
Solution :

The measure of longest side = √75

a = √75, b = √48 and c = √27

Using Pythagorean theorem.

 (√75)² = (√48)² + (√27)²

75 = 48 + 27

75 = 75

So, it is a right triangle.

Problem 6 :

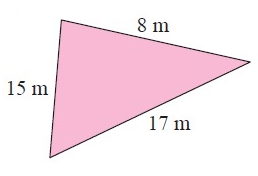
Solution :

The measure of longest side = √75

a = √75, b = √48 and c = √27

Using Pythagorean theorem.

17² = 15² + 8²

289 = 225 + 64

289 = 289

So, it is a right triangle.