DETERMINE IF THE TABLE REPRESENTS LINEAR OR EXPONENTIAL FUNCTION

Decide whether the table represents a linear or exponential function. Then, write the function formula.

Problem 1 :

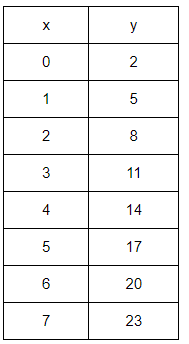
Solution :

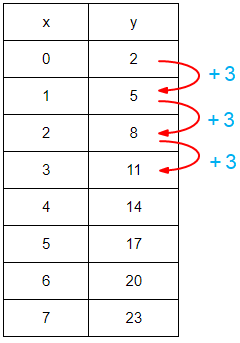
To get values of y, we have to add 3. Then, it is linear function.

Linear function will be in the form of y = mx + b

Slope(m) = 3 and y-intercept (b) = 2

So, the required function is y = 3x + 2

Problem 2 :

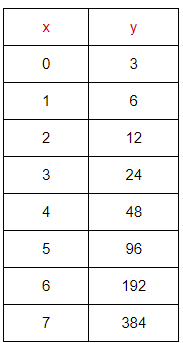
Solution :

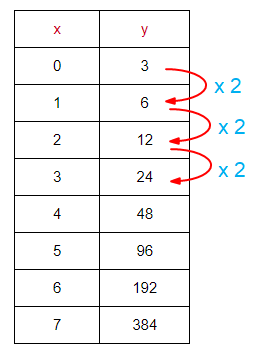
Since the multiplication factor is the same and it is greater than 1, it is exponential growth function.

Exponential function will be in the form of y = a(b)^x

Initial value (a) = 3

Multiplication factor (b) = 2

So, the required exponential function is y = 3(2)^x

Problem 3 :

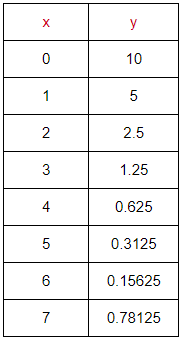
Solution :

Observing the values of y,

10/2 ==> 5

5/2 ==> 2.5

Since the multiplication factor is 1/2, that is lesser than 1. It should be exponential decay function

Exponential function will be in the form of y = a(b)^x

Initial value (a) = 10

Multiplication factor (b) = 1/2

So, the required exponential function is y = 10(1/2)^x

Identify the function as linear or exponential and determine the slope or growth factor. Write the rule for each function and sketch a graph labeling the y-intercept.

Problem 4 :

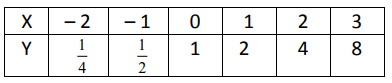
Solution :

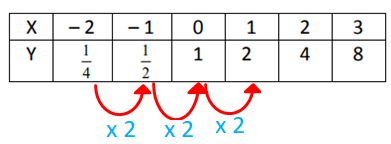
Since the multiplication factor is same and it is greater than 2. It is exponential growth function.

Multiplication factor = 2

Exponential function will be in the form of y = a(b)^x

Initial value (a) = 1

So, the required exponential function is y = 1(2)^x

Problem 5 :

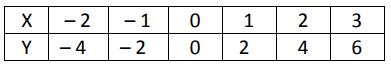
Solution :

By observing the values of y, it is added by 2.

-4 + 2 ==> -2

-2 + 2 ==> 0

0 + 2 ==> 2

y = -4x + 2

It is a linear function .

Problem 6 :

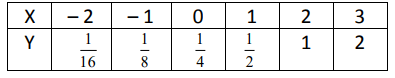
Solution :

By observing the values of y, it is multiplied by 2

(1/16) x 2 ==> 1/8

(1/8) x 2 ==> 1/4

(1/4) x 2 ==> 1/2

(1/2) x 2 ==> 1

Multiplication factor = 2

a = 1/4 and b = 2

y = (1/4)(2)^x

It is a exponential function.

Problem 7 :

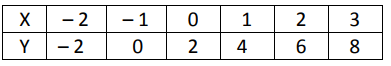
Solution :

By observing the values of y, it is added by 2

-2 + 2 ==> 0

0 + 2 ==> 2

2 + 2 ==> 4

y-intercept = 2

y = 2 + 2x

It is a linear function.