DETERMINE IF THE LINES ARE PARALLEL PERPENDICULAR OR NEITHER

Tell whether the lines are parallel, perpendicular, or neither.

Problem 1 :

Line 1 : through (-3, -7) and (1, 9)

Line 2 : through (-1, -4) and (0, -2)

Solution :

They are not parallel, they are not perpendicular. So, the lines are neither.

Problem 2 :

Line 1 : through (2, 7) and (-1, -2)

Line 2 : through (3, -6) and (-6, -3)

Solution :

m₁ x m₂ = 3 (-1/3)

m₁ x m₂ = -1

So, the lines are perpendicular.

Determine whether the graphs of each pair of equations are parallel, perpendicular, or neither.

Problem 3 :

y = 3x + 4

y = 3x + 7

Solution :

y = 3x + 4 ----- (1)

y = 3x + 7 ------(2)

Comparing the above equations with slope intercept form

y = mx + b, we get 

m₁ = 3, m₂ = 3

b₁ = 4, b₂ = 7

Both lines are having same slope.  but different y – intercepts. So, the given lines are parallel. 

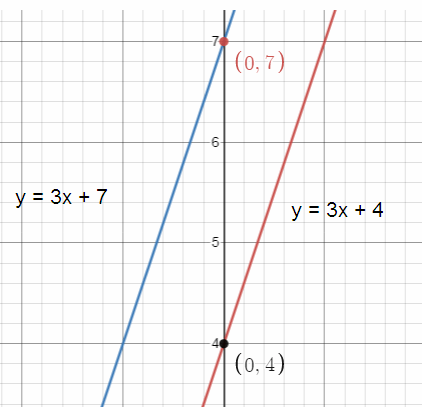
Problem 4 :

y = -4x + 1

4y = x + 3

Solution :

y = -4x + 1 ------(1)

4y = x + 3

y = x/4 + 3/4   ------(2)

m = -4, m = 1/4

m₁ ⋅ m₂ = -4 (1/4)

m₁ ⋅ m₂ = -1

Since the product of the slopes is equal to -1. The lines are perpendicular. 

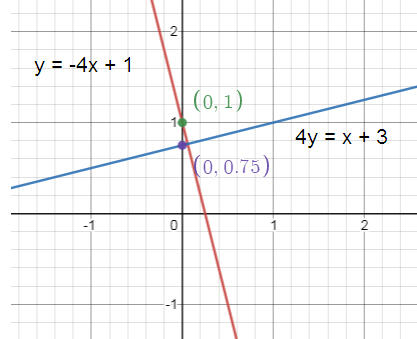
Problem 5 :

y = 2x - 5

y = 5x - 5

Solution :

y = 2x – 5   -----(1)

y = 5x - 5  -----(2)

Comparing (1) and (2)

 y = mx + b

m = 2, m = 5

b = -5, b = -5

There is no relationship between slopes, so they are neither.

Problem 6 :

y = -1/3x + 2

y = 3x - 5

Solution :

y = -1/3x + 2  -----(1)

y = 3x - 5 -----(2)

 y = mx + b

m₁ = -1/3, m₂ = 3

b = 2, b = -5

m₁ = -1/3, m₂ = 3

m₁ ⋅  m₂ = (-1/3) ⋅ 3

Product of the slope is equal to -1. So, the lines are perpendicular.

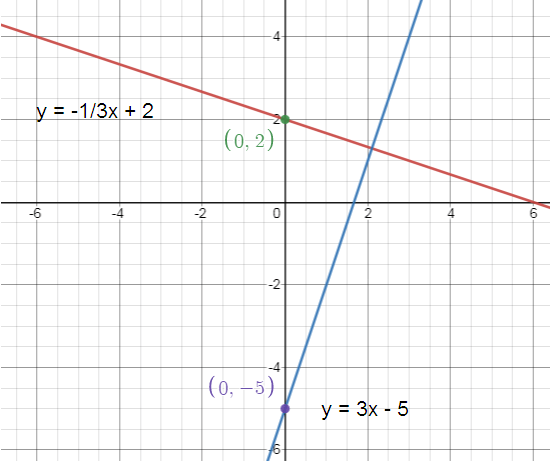
Problem 7 :

y = 3/5x - 3

5y = 3x - 10

Solution :

y = 3/5x – 3 ------(1)

5y = 3x - 10

y = 3/5x - 10 ------(2)

 y = mx + b

m₁ = 3/5, m₂ = 3/5

b = -3, b = -10

Both lines have the same slope but have different y-intercepts. So, the lines are parallel.

Problem 8 :

y = 4

4y = 6

Solution :

y = 4 ------(1)

4y = 6

y = 6/4

y = 3/2------(2)

Both are horizontal lines and they will not intersect.