DETERMINE IF THE GRAPH IS A FUNCTION THEN STATE THE DOMAIN AND RANGE

State the domain and range for each graph and then tell if the graph is a function.

Problem 1 : 

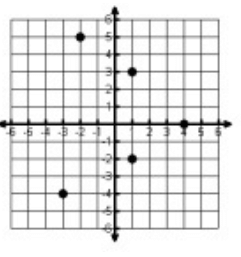
Solution :

Writing the points marked above, we get

(-3, -4) (-2, 5) (1, 3) (1, -2) (4, 0)

Domain = {-3, -2, 1, 4}

Range = {-4, -2, 0, 3, 5}

Here 1 is having more than one output, it is not a function.

Problem 2 :

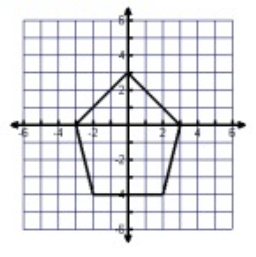
Solution :

Between -3 to 3, the graph is spreading over the x-axis.

Domain = -3 ≤ x ≤ 3

Between -4 to 3, the graph is spreading over the y-axis.

Range = -4 ≤ y ≤ 3

By drawing the vertical line, that will intersect the curve at more than one point. So, it is not a function.

Problem 3 :

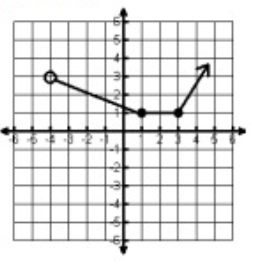
Solution :

Between -4 to ∞, the graph is spreading over the x-axis. Since we have open circle at -4, we have to use open circle.

Domain = -4 < x < ∞

Between 1 to ∞, the graph is spreading over the y-axis. 

Range = 1 ≤ y < ∞

By drawing the vertical line, that will intersect the curve at one point. So, it is a function.

Problem 4 :

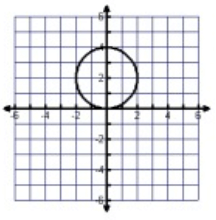
Solution :

Between -2 to 2, the graph is spreading over the x-axis.

Domain = -2 ≤ x ≤ 2

Between 0 to 4, the graph is spreading over the y-axis.

Range = 0 ≤ y ≤ 4

By drawing the vertical line, that will intersect the curve at more than one point. So, it is not a function.

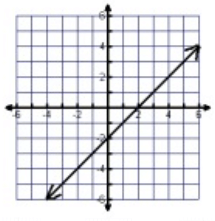
Problem 5 :

Solution :

Between -∞ to ∞, the graph is spreading over the x-axis. 

Domain = All real numbers

Between -∞ to ∞, the graph is spreading over the y-axis. 

Range = All real numbers

By drawing the vertical line, that will intersect the curve at one point. So, it is a function.

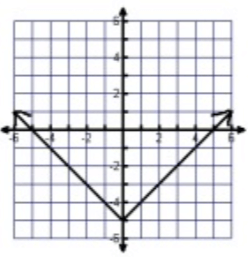
Problem 6 :

Solution :

Between -∞ to ∞, the graph is spreading over the x-axis. 

Domain = All real numbers

Between -5 to ∞, the graph is spreading over the y-axis. 

Range = -5 ≤ y ≤ ∞

By drawing the vertical line, that will intersect the curve at one point. So, it is a function.

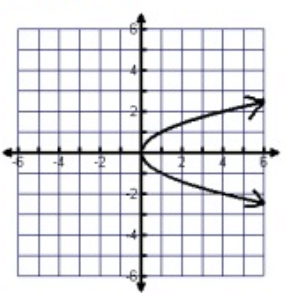
Problem 6 :

Solution :

Between 0 to ∞, the graph is spreading over the x-axis. 

Domain = 0 ≤ x ≤ ∞

Between -∞ to ∞, the graph is spreading over the y-axis. 

Range = -∞ ≤ y ≤ ∞

By drawing the vertical line, that will intersect the curve at more than one point. So, it is not a function.

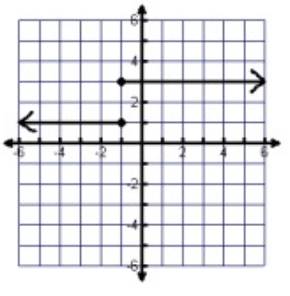
Problem 8 :

Solution :

Domain = All real values

Range = {1, 3}

For -1, we have two different outputs 1 and 3. So, it is not a function.