DETERMINE IF A FUNCTION IS LINEAR QUADRATIC OR CONSTANT

Determine whether each function is linear or quadratic. Identify the quadratic, linear, and constant terms.

Problem 1 :

y = (x – 2)(x + 4)

Solution :

It is in factored form.

y = x² + 4x - 2x - 8

y = x² + 2x - 8

The degree of the polynomial is 2. So, it is quadratic.

Problem 2 :

y = 3x(x + 5)

Solution :

y = 3x(x + 5)

Distributing 3x, we get

y = 3x² + 15x

Degree of the polynomial is 2. So, it is quadratic polynomial.

Problem 3 :

y = 5x(x – 5) –5x²

Solution :

y = 5x(x – 5) –5x²

y = 5x² – 5x –5x²

By combining the like terms, we get

y = – 5x

Degree of this polynomial is 1. So, it is a linear.

Problem 4 :

f(x) = 7(x – 2) + 5(3x)

Solution :

f(x) = 7(x – 2) + 5(3x)

f(x) = 7x - 14 + 15x

By combining the like terms

f(x) = 22x - 14

The degree of the polynomial is 1. So it is linear.

Problem 5 :

f(x) = 3x² – (4x – 8)

Solution :

f(x) = 3x² – (4x – 8)

f(x) = 3x² – 4x + 8

Degree of the f(x) is 2. So, it is quadratic polynomial.

Problem 6 :

y = 3x(x – 1) – (3x + 7)

Solution :

y = 3x(x – 1) – (3x + 7)

y = 3x² - 3x - 3x - 7

By combining the like terms, we get

y = 3x² - 6x - 7

The degree of the polynomial is 2. So, it is quadratic.

Problem 7 :

y = 3x² – 12

Solution :

The degree of the polynomial is 2. So, it is quadratic.

Problem 8 :

f(x) = (2x – 3)(x + 2) 

Solution :

The degree of the polynomial is 2. So, it is quadratic.

Identify Linear, Quadratic, and Exponential functions from Tables

You can use patterns between consecutive data pairs to determine which type of function models the data. The differences of consecutive y-values are called first differences. The differences of consecutive first differences are called second differences.

• Linear Function The first differences are constant.

• Exponential Function Consecutive y-values have a common ratio.

• Quadratic Function The second differences are constant. In all cases, the differences of consecutive x-values need to be constant.

Tell whether each table of values represents a linear, an exponential, or a quadratic function.

Problem 9 :

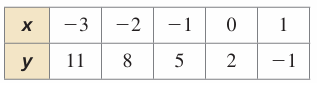
Solution :

The first differences are constant, then the given table must be in linear function.

Problem 10 :

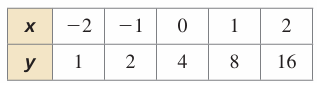
Solution :

Consecutive y-values have a common ratio. So, the table represents an exponential function.

Problem 11 :

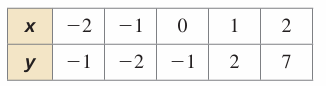
Solution :

Relationship between x-values :

-2 + 1 ==> -1

-1 + 1 ==> 0

0 + 1 ==> 1

1 + 1 ==> 2

Relationship between y-values :

The second differences are constant. So, the table represents a quadratic function.

Tell whether the points appear to represent a linear, an exponential, or a quadratic function.

Problem 12 :

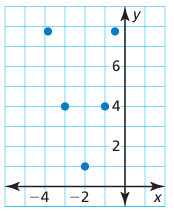
Solution :

By connecting the points, we will get the graph of parabola. So, it must be a quadratic function.

Problem 13 :

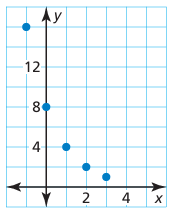
Solution :

By connecting the points, we will get the graph of exponential decreasing. So, it must be a exponential function.

\Problem 14 :

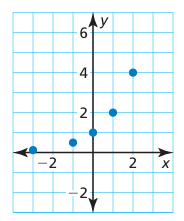
Solution :

By connecting the points, we will get the graph of exponential increasing. So, it must be a exponential function.

Problem 15 :

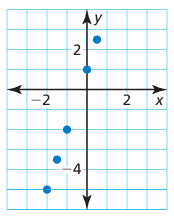
Solution :

By connecting the points, we will get the graph of straight line. So, it must be a linear function.

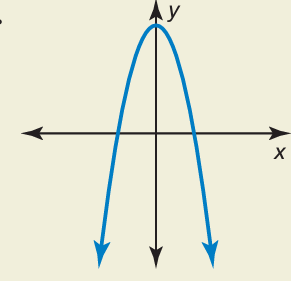
Problem 16 :

Match each graph with its function. Explain your reasoning.

a) y = 2x² − 4     b) y = 2^x − 1      c)  y = 2x − 1     d)  y = −2x² + 4

Solution :

	The graph shows a parabola which opens down, then the leading coefficient will have negative sign. So option d)  y = −2x2 + 4 is correct.
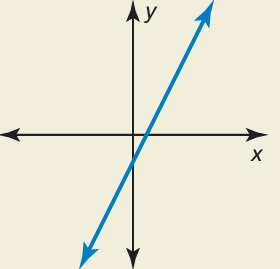
	The graph shows a straight line. So, option c) y = 2x − 1 is correct.
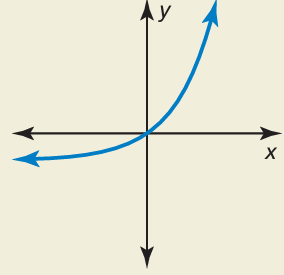
	The graph shows exponential function. So, option b) y = 2x − 1 is correct.
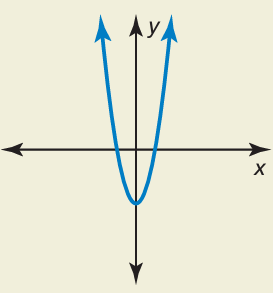
	The graph shows a parabola which opens up, then the leading coefficient will have positive sign. So option a) y = 2x2 − 4 is correct.