DETERMINE IF A FUNCTION IS CONTINUOUS AT A POINT

Problem 1 :

continuous at x = -1 and continuous at x = 2 ?

Solution :

If the function is continuous at x = -1, then

lim _{x -> -1}^- f(x) = lim _{x -> -1}⁺ f(x)

So, the function is continuous at x = -1.

If the function is continuous at x = 2, then

lim _{x -> 2}^- f(x) = lim _{x -> 2}⁺ f(x)

So, the function is not continuous at x = 2.

Problem 2 :

continuous at x = 1 ?

Solution :

So, the function g(x) is not continuous at x = 1.

Problem 3 :

Solution :

Checking if it is continuous at x = -3 :

Checking if it is continuous at x = 4 :

The function is not continuous at x = -3 and continuous at x = 4.

Problem 4 :

Solution :

Checking if it is continuous at x =  π/2 :

Since the left hand limit and right hand limit they are not equal, f(x) is not continuous at x =  π/2

Checking if it is continuous at x =  π :

So, the function f(x) is not continuous at x=π/2 and continuous at x = π.

Problem 5 :

The function f has the properties indicated in the table below. Which of the following must be true ?

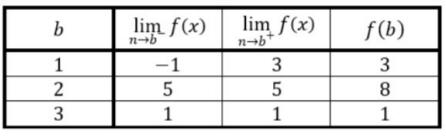
a)  f is continuous at x = 1        b)  f is continuous at x = 2

c)  f is continuous at x = 3        d)  None of the above.

Solution :

By observing the table, at x -> 3

lim _x->3^- f(x) and lim _x->3⁺ f(x) they are equal. So, the function f(x) is continuous at x --> 3

Problem 6 :

If the function f is continuous for all real numbers and if 

f(x) = (x² - 4)/(x + 2)

when x ≠ 2, then f(-2) =

A) -4   B)  -2   C)  -1  D) 0   E) 2

Solution :

f(x) = (x² - 4)/(x + 2)

f(x) = (x² - 2²)/(x + 2)

= (x + 2)(x - 2) / (x + 2)

f(x) = (x - 2)

f(-2) = -2 - 2

= -4

So, the answer is -4.

Problem 7 :

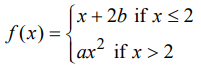
Let f be the function given above. What are all values of a and b for which f is differentiable at x = 2 ?

a) 1/4 and b = -1/2

b)  a = 1/4 and b = 1/2

c)  a = 1/4 and b is any real number]

d)  a = b + 2 where b is any real number

e)  There are no such values of a and b.

Solution :

lim _x->2- f(x) = lim _x->2- x + 2b

= 2 + 2b ----(1)

lim _x->2+ f(x) = lim _x->2+ ax²

= a(2)²

= 4a ----(2)

Since it is differentiable at x = 2

lim _x->2 f(x) = f'(2)

f'(x) = 1 + 2(0)

f'(2) = 1  ----(3)

So, option a is correct.