DETERMINE GRAPHICALLY OR ALGEBRAICALLY IF A FUNCTION IS ODD OR EVEN
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A Function can be classified as Even, Odd or Neither. This classification can be determined graphically or algebraically.
How to check if the graph is odd ?
The graph will be symmetric with respect to the origin.
In other words :
If you spin the picture upside down about the Origin, the graph looks the same!
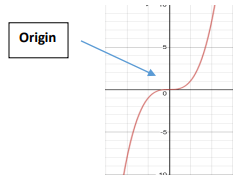
How to check if the graph is even ?
The graph will be symmetric with respect to the y-axis.
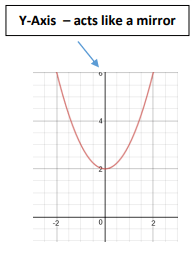
Properties of odd and even functions :
Properties of odd function :
- The graph is symmetric about origin.
- The exponents of all terms in its equation are odd.
Properties of even function :
- The graph is symmetric about y-axis.
- The exponents of all terms in its equation are even.
Algebraically Check if it is odd or even
A function f is even when, for each x in the domain of f,
f(-x) = f(x).
A function f is odd when, for each x in the domain of f,
f(-x) = -f(x).
Graphically Checking If the Function is Odd or Even
Determine graphically using possible symmetry, whether the following functions are even, odd or neither.
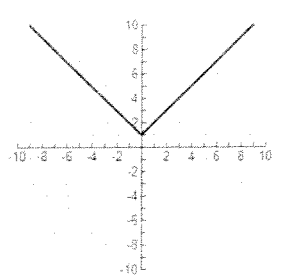
Problem 1 :
Solution :
The graph is not symmetric about origin, then it is not odd function.
The graph is not symmetric about y-axis, then it is not even function.
So, it is neither.
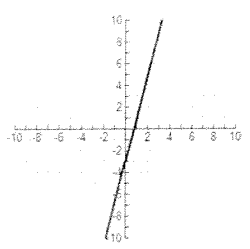
Problem 2 :
Solution :
Here y-axis is acting as a mirror. Clearly it is symmetric about y-axis. Then, it is even function.
Problem 3 :
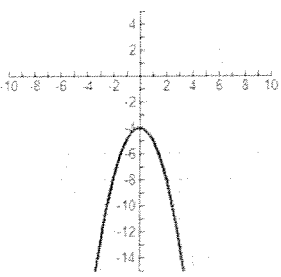
Solution :
Here y-axis is acting as a mirror. Clearly it is symmetric about y-axis. Then, it is even function.
Problem 4 :
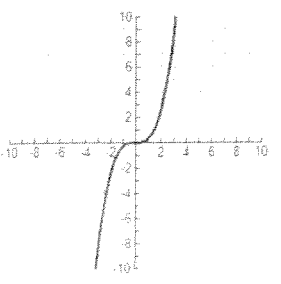
Solution :
The graph is symmetric about origin. So, it is odd function.
Problem 5 :
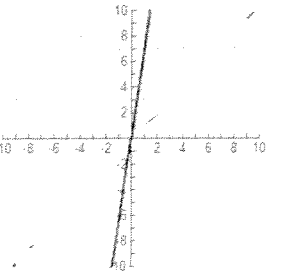
Solution :
The graph is not symmetric about origin, then it is not odd function.
The graph is not symmetric about y-axis, then it is not even function.
So, it is neither.
Problem 6 :
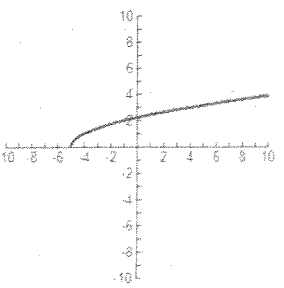
Solution :
The graph is not symmetric about origin, then it is not odd function.
The graph is not symmetric about y-axis, then it is not even function.
So, it is neither.
Problems on Algebraically Checking If It is Odd or Even
Verify algebraically whether each function is even, odd or neither!
Problem 1 :
f(x) = x3 - 6x
Solution:
f(x) = x3 - 6x
Put x = -x
f(-x) = (-x)3 - 6(-x)
= -x3 + 6x
So, it is neither.
Problem 2 :
g(x) = x4 - 2x2
Solution:
g(x) = x4 - 2x2
Put x = -x
g(-x) = (-x)4 - 2(-x)2
= x4 - 2x2
So, it is even function.
Problem 3 :
h(x) = x2 + 2x + 1
Solution:
h(x) = x2 + 2x + 1
Put x = -x
h(-x) = (-x)2 + 2(-x) + 1
= x2 - 2x + 1
h(-x) ≠ h(x)
So, it is neither.
Problem 4 :
f(x) = x2 + 6
Solution:
f(x) = x2 + 6
Put x = -x
f(-x) = (-x)2 + 6
= x2 + 6
f(-x) = f(x)
So, it is even function.
Problem 5 :
g(x) = 7x3 - x
Solution:
g(x) = 7x3 - x
Put x = -x
g(-x) = 7(-x)3 - (-x)
= -7x3 + x
g(-x) ≠ g(x)
So, it is odd function.
Problem 6 :
h(x) = x5 + 1
Solution:
h(x) = x5 + 1
Put x = -x
h(-x) = (-x)5 + 1
= -x5 + 1
h(-x) ≠ h(x)
So, it is neither.
Problem 7 :
f(x) = x√(4 - x2)
Solution:
f(x) = x√(4 - x2)
Put x = -x
f(-x) = (-x)√(4 - (-x)2)
= -x√(4 - x2)
So, it is neither.
Problem 8 :
g(x) = x4√(1 + x)
Solution:
g(x) = x4√(1 + x)
Put x = -x
g(-x) = (-x)4√(1 + (-x))
= x4√(1 - x)
So, it is neither.
Problem 9 :
h(x) = |x| - 1
Solution:
h(x) = |x| - 1
Put x = -x
h(-x) = |-x| - 1
= x - 1
So, it is even function.
Problem 10 :
Solution:
So, it is even function.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling