DESCRIBING TRANSFORMATIONS OF QUADRATIC FUNCTIONS

Find the following for the quadratic functions below.

Vertex:

Transformations:

Domain :

Range :

Max/min:

Axis of symmetry:

y-intercept:

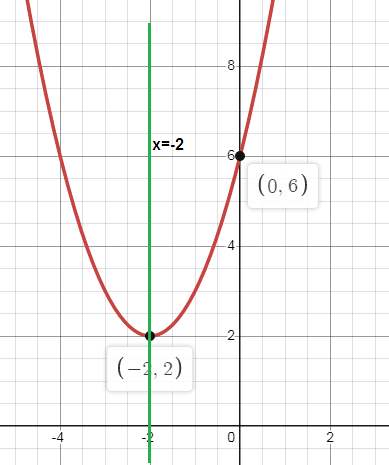
Problem 1 :

y = (x + 2)² + 2

Solution:

Vertex:

y = a(x - h)² + k

y = (x + 2)² + 2

Vertex (h, k) = (-2, 2)

Transformations: 

Parent function is shifted 2 units left and 2 units up.

Domain:

All real numbers.

x € R

Range:

y ≥ 2

 {y € R|  y ≥ 2}

Max/min:

Min = 2

Axis of symmetry:

x = h

x = -2

y-intercept:

set x = 0

y = (0 + 2)² + 2

y = 4 + 2

y = 6

y-intercept = (0, 6)

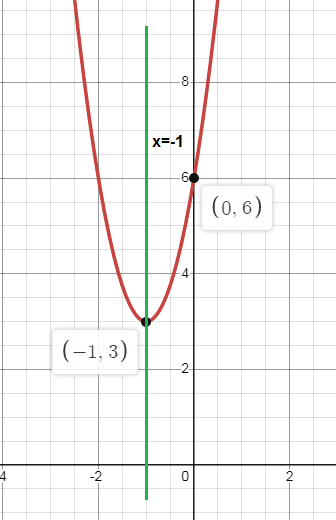
Problem 2 :

y = 3(x + 1)² + 3

Solution:

Vertex:

y = a(x - h)² + k

y = 3(x + 1)² + 3

Vertex (h, k) = (-1, 3)

Transformations: 

Parent function is vertically stretched by shifted 1 unit left and 3 units up.

Domain:

All real numbers.

x € R

Range:

y ≥ 3

 {y € R|  y ≥ 3}

Max/min:

Min = 3

Axis of symmetry:

x = h

x = -1

y-intercept:

set x = 0

y = 3(0 + 1)² + 3

y = 3 + 3

y = 6

y-intercept = (0, 6)

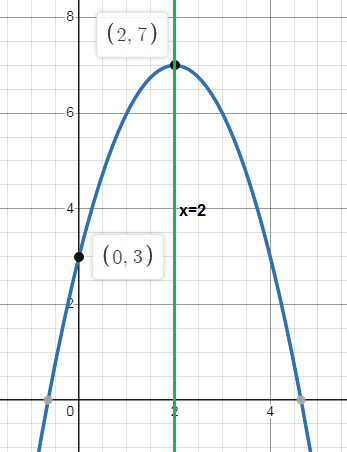
Problem 3 :

y = -(x - 2)² + 7

Solution:

Vertex:

y = a(x - h)² + k

y = -(x - 2)² + 7

Vertex (h, k) = (2, 7)

Transformations: 

Parent function is inverted about the x-axis. shifted 2 units right and 7 units up.

Domain:

All real numbers.

x € R

Range:

y ≤ 7

{y € R|  y ≤ 7}

Max/min:

Max = 7

Axis of symmetry:

x = h

x = 2

y-intercept:

set x = 0

y = -(0 - 2)² + 7

y = -4 + 7

y = 3

y-intercept = (0, 3)

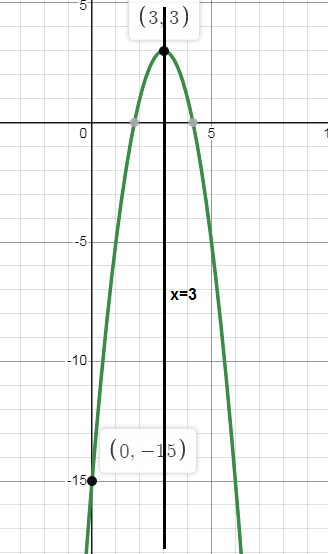
Problem 4 :

y = -2(x - 3)² + 3

Solution:

Vertex:

y = a(x - h)² + k

y = -2(x - 3)² + 3

Vertex (h, k) = (3, 3)

Transformations: 

Parent function is vertically stretched by shifted 3 units right and 3 units up.

Domain:

All real numbers.

x € R

Range:

y ≤ 3

{y € R|  y ≤ 3}

Max/min:

Max = 3

Axis of symmetry:

x = h

x = 3

y-intercept:

set x = 0

y = -2(0 - 3)² + 3

y = -18 + 3

y = -15

y-intercept = (0, -15)

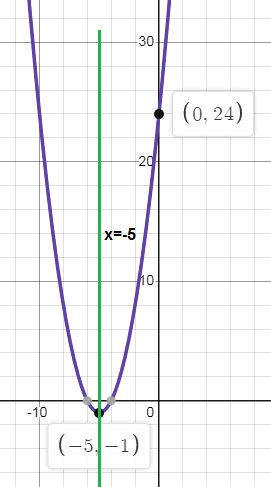
Problem 5 :

y = (x + 5)² - 1

Solution:

Vertex:

y = a(x - h)² + k

y = (x + 5)² - 1

Vertex (h, k) = (-5, -1)

Transformations: 

Parent function is shifted 5 units left and 1 unit down.

Domain:

All real numbers.

x € R

Range:

y ≥ -1

{y € R|  y ≥ -1}

Max/min:

Min = -1

Axis of symmetry:

x = h

x = -5

y-intercept:

set x = 0

y = (0 + 5)² - 1

y = 24

y-intercept = (0, 24)

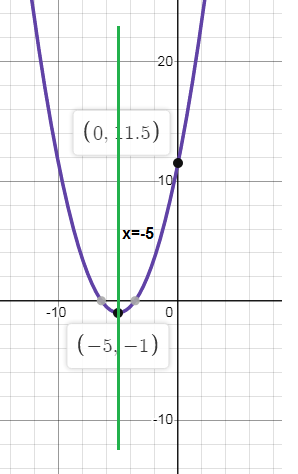
Problem 6 :

y = 1/2(x + 5)² - 1

Solution:

Vertex:

y = a(x - h)² + k

y = 1/2(x + 5)² - 1

Vertex (h, k) = (-5, -1)

Transformations: 

Parent function is vertically stretched by 5 units left and 1 unit down.

Domain:

All real numbers.

x € R

Range:

y ≥ -1

{y € R|  y ≥ -1}

Max/min:

Min = -1

Axis of symmetry:

x = h

x = -5

y-intercept:

set x = 0

y = 1/2(0 + 5)2 - 1

y = 11.5

y-intercept = (0, 11.5)