DESCRIBING THE TRANSFORMATION OF LINEAR FUNCTION

For any function f(x), not just linear, there are four ways that we can transform it. We can add something to the input or the output, or we can multiply something by the input or the output. Let’s take each one individually.

Given 𝒇(𝒙) = 𝒙, describe the transformation shown by each equation.

Problem 1 :

g(𝑥) = 𝑥 − 5

Solution :

Comparing with the parent function f(x), the function g(x) x is subtracted with 5 or the entire function is subtracted with 5. There are two way of understanding in this.

Horizontal translation :

Horizontally move 5 units to the right.

(or)

Vertical translation :

Vertically move down 5 units.

Problem 2 :

g(𝑥) = 𝑥 + 4

Solution :

g(𝑥) = 𝑥 - (-4)

Comparing with the parent function f(x), the function g(x) x is added with 4 or the entire function is added with 4. There are two understanding in this.

Horizontal translation :

Horizontally move 4 units left.

(or)

Vertical translation :

Vertically move up 4 units.

Problem 3 :

g(𝑥) = 3𝑥

Solution :

g(𝑥) = 3𝑥

Comparing with parent function y = f(x), 3 is multiplied with the function, vertical stretch with the factor of 3.

Problem 4 :

g(𝑥) = (1/2)𝑥

Solution :

g(𝑥) = (1/2)𝑥

Comparing with parent function y = f(x), 1/2 is multiplied with the function, vertical shrink with the factor of 1/2.

Problem 5 :

g(𝑥) = -x + 1

Solution :

g(𝑥) = -x + 1

We have negative coefficient, so there is reflection across y-axis. Since it is added with 1, we have to move the graph 1 unit up after reflection.

Problem 6 :

g(𝑥) = (1/10)x - 2

Solution :

g(𝑥) = (1/10)x - 2

1/10 lies between 0 to 1, we will have vertical shrink with the factor of 1/10 and shifting down the curve 2 units.

Problem 7 :

The graph of 𝑓(𝑥) is shown on the coordinate plane. Sketch 𝑔(𝑥) which is steeper than 𝑓(𝑥) by a factor of 2, and is shifted down units.

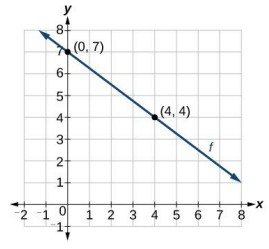
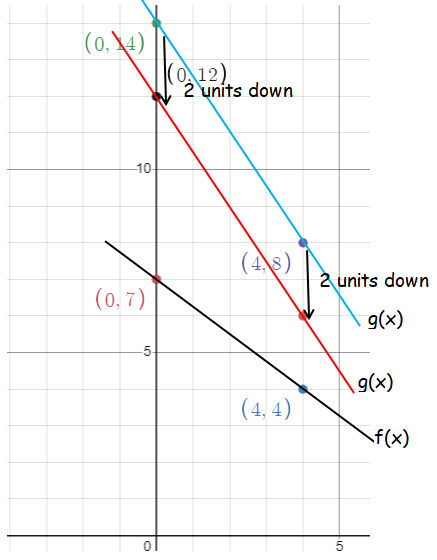
Solution :

Taking two points from the line shown are (0, 7) and (4, 4). Since the new line should be more steeper than the line shown f, we have to multiply each y-coordinate by 2.

Problem 8 :

The graph of 𝑓(𝑥) is shown on the coordinate plane. Sketch 𝑔(𝑥) which is steeper than 𝑓(𝑥) by a factor of 2, and is shifted down units.

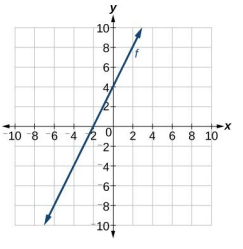
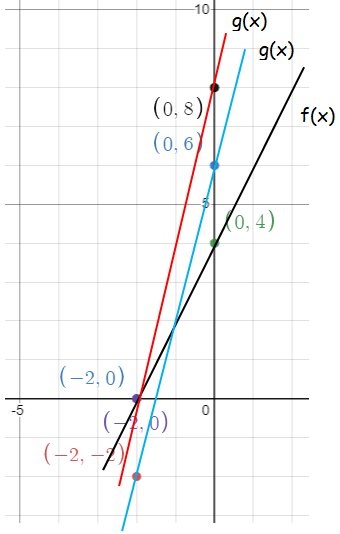
Solution :

Taking two points from the line shown are (-2, 0) and (0, 4). Since the new line should be more steeper than the line shown f, we have to multiply each y-coordinate by 2.