DESCRIBING THE TRANSFORMATION OF A EXPONENTIAL FUNCTION

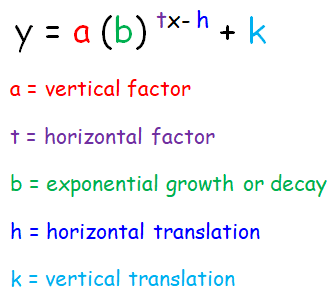
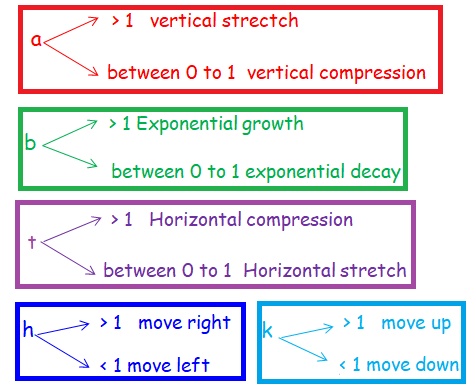
Describe the transformation that map the function y = 2^x on each of the following functions.

Problem 1 :

y = 2^x - 2

Solution :

Comparing the given with the standard form of exponential function

y = a (b)^{x - h} + k

a = 1, b = 2, h = 0 and k = -2

The value of k tells us about the vertical translation. Here the value of k is -2 < 0, so we have to move the curve down 2 units.

Required transformation is,

shifting 2 units down

Problem 2 :

y = 2^x+3 

Solution :

Comparing the given with the standard form of exponential function

y = a (b)^{x - h} + k

y = 2^{x - (-3)} 

a = 1, b = 2, h = -3 and k = 0

The value of k tells us about the horizontal translation. Here the value of h is -3 < 0, so we have to move the curve left 3 units.

Required transformation is,

shifting 3 units left

Problem 3 :

y = 4^x 

Solution :

The given function is not in terms of the parent function.

y = (2²)^x

The value of x is being multiplied by 2, so it should be horizontal stretch or compression. 

Considering the value of a = 2 > 1, this should be horizontal compression.

Required transformation is,

horizontal compression by the factor of 2.

Problem 4 :

y = 3(2^{x - 1}) + 1

Solution :

Comparing the given with the standard form of exponential function

y = a (b)^{x - h} + k

a = 3, b = 2, h = 1 and k = 1

Transformations should be done in the following order.

1) compression or stretches

2) Reflection

3) translation

So, the required transformations are,

a = 3 >1, so vertical stretch with the factor of 3.

No reflection

  Translation of 1 unit right and 1 unit up.

Describe the transformation that map into the function

y = 8^x

on to each function.

Problem 5 :

y = (1/2) 8^x

Solution :

Comparing the given with the standard form of exponential function

y = a (b)^{x - h} + k

a = 1/2

comparing with the parent function, the value of b is the same and no translation.

The value of a tells us the vertical stretch or compressions.

Considering the value of a = 1/2  ==> 0 < b < 1

So, the required transformation is,

vertical compression by the factor of 1/2.

Problem 6 :

y = -8^x

Solution :

y is changed as -y, so reflection across x-axis.

So, the required transformation is,

reflection across x-axis.

Problem 7 :

y = 8^-2x

Solution :

Scale factor is 2, horizontal compression with the factor of 2.

x is changed as -x, so reflection across y-axis.

So, the required transformation is,

horizontal compression with reflection across y-axis.

Using the parent graph of f(x) = 4^x, describe the transformation of each function.

Problem 8 :

f(x) = -2(4^{x + 3}) - 5

Solution :

f(x) = -2(4^{x - (-3)}) - 5

Here, a = -2, b = 4 (same), h = -3 and k = -5

Vertical stretch with the factor with the of 2 along with reflection across x-axis.

Horizontal translation of 3 units left and vertical translation of 5 units down.

So, the required transformations are,

Vertical stretch of factor 2 ==> reflection across x-axis => move left 3 units and down 5 units.

Problem 9 :

f(x) = (4^{2x + 6}) + 2

Solution :

f(x) = (4^{2x - (-6)}) + 2

Here, a = 1, b = 4 (same), h = -6 and k = 2

So, the required transformations are,

Horizontal compression of 2 units. No reflection. Move horizontally 6 units left and 2 unit up.

Problem 10 :

f(x) = (4^{-3x + 12}) + 1

Solution :

f(x) = (4^{-3x - (-12)}) + 1

Here, a = 1, b = 4 (same), h = -12 and k = 1

So, the required transformations are,

horizontal factor of 3, 3 > 1

Horizontal compression of 3 units. Reflection across y-axis. Move  horizontally 12 units left and 1 unit up.

Problem 11 :

f(x) = (4^{(1/2)x - 2}) + 3

Solution :

f(x) = (4^{(1/2)x - 2}) + 3

Here, a = 1, b = 4 (same), h = 2 and k = 3

So, the required transformations are,

horizontal factor of 1/2, 0 < HF < 1

Horizontal stretch of 1/2 units. No reflection. Move  horizontally 2 units right and 3 units up.

Problem 12 :

f(x) = (1/3)(4^{(1/3)x + 3}) - 4

Solution :

f(x) = (1/3)(4^{(1/3)x + 3}) - 4

Here, a = 1/3, b = 4 (same), h = -3 and k = -4

So, the required transformations are,

horizontal factor of 1/3, 0 < HF < 1

Horizontal stretch of 1/3 units. No reflection. Move  horizontally 3 units left and 4 units down.