DESCRIBING THE FUNCTION AS LINEAR OR EXPONENTIAL FUNCTION

Linear function increase by a constant slope  but exponential equations increase by a constant exponent or power.

Linear function will be in the form

y = mx + b

Exponential function will be in the form

y = ab^x

(or)

y = ab^x-h + k

Linear function		Exponential function

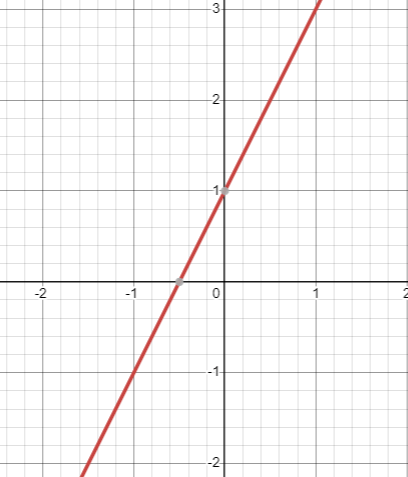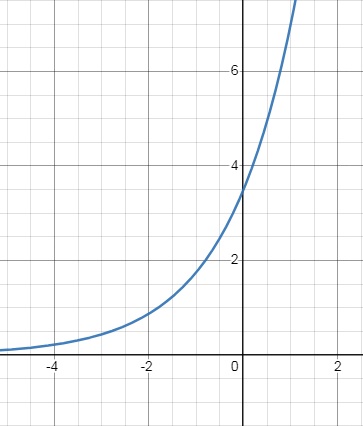Describe each function as a linear function or exponential function.

Problem 1 :

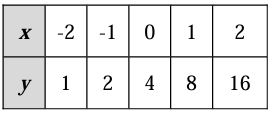
Solution :

Values of x is increasing by 1, values of y 

1 x 2 = 2

2 x 2 = 4

4 x 2 = 8

Every values of y is multiplied by 2. Since the multiplication factor is the same, it must be exponential function.

Finding the exponential function :

y = ab^x ----(1)

b = 2

From the table, applying the point (0, 4), we get

4 = a(2)^-0

4 = a(1)

a = 4

By applying the value of a and b in (1), we get

y = 4(2)^x 

Problem 2 :

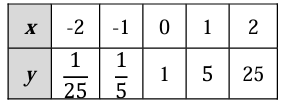
Solution :

Values of x is increasing by 1, values of y 

 (1/25) / (1/5) = 1/5

(1/5) / 1 = 1/5

1/5

Every values of y is multiplied by 1/5. Since the multiplication factor is the same, it must be exponential function.

Finding the exponential function :

y = ab^x ----(1)

b = 1/5

From the table, applying the point (0, 1), we get

1 = a(1/5)^-0

1 = a(1)

a = 1

By applying the value of a and b in (1), we get

y = 1(1/5)^x 

y = (1/5)^x 

Problem 3 :

y = -6x + 9

Solution :

y = -6x + 9

The given function is in the form,

y = mx + b

Here m = -6 and b = 9

Problem 4 :

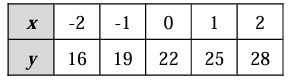
Solution :

Considering the values of x, it is increased by 1. 

Considering the values of y, it is increased by 3.

Finding the linear function :

y = mx + b

m = 3

y = 3x + b ----(1)

Applying the point (0, 22), we get

22 = 3(0) + b

22 = 0 + b

b = 22

Applying the value of b in (1), we get

y = 3x + 22

Problem 5 :

y = 3 (2)^x 

Solution :

The given function in the form, y = ab^x. Then it is exponential function.

Problem 6 :

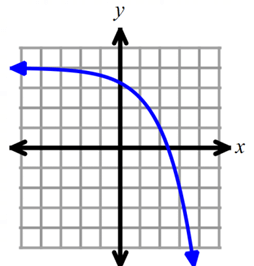
Solution :

The given graph is the graph of exponential function.

y = ab^{x - h} + k 

Here y = k is the horizontal asymptote. From the given graph, horizontal asymptote is y = 4

k = 4

By applying the of k, we get

y = ab^{x - h} + 4 

By choosing three points from the graph, we can get the values of a, b and h. 

Problem 7 :

Select which exponential function below models this situation: Lupe bought a gold chain for $350, and the value of the chain increases by 4% per year. Use 𝑦 for the value of the chain and 𝑡 for the time in years.

A) 𝑦 = 350^4𝑥       B) 𝑦 = 350(4)^𝑥

C) 𝑦 = 350(1.4)^𝑥      D) 𝑦 = 350(1.04)^𝑥

Solution :

Every year the value of the chain increase by the constant factor. 

Since the growth factor is the same, it must be a exponential function.

y = a(1 + r%)^x

Growth factor = 4%

a = 350

y = 350(1 + 4%)^x

= 350(1 + 0.04)^x

= 350(1.04)^x

So, option D is correct.

Problem 8 :

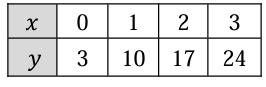
Solution :

The values of x is increasing by 1. By observing the values of y, it is increased by 7.

Constant rate of change is 7,

Creating exponential function :

y = mx + b

y = 7x + b --------(1)

By choosing the point (0, 3) and applying this point in the above function

3 = 7(0) + b

3 = 0 + b

b = 3

By applying the value of b in (1), we get

y = 7x + 3

Problem 9 :

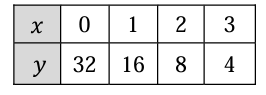
Solution :

By observing the values of x is increased by 1, by observing the values of y, we get

32/16 = 2

16/8 = 2

8/4 = 2

Since the constant factor is the same, it must be an exponential function.

y = ab^x ----(1)

Applying the point (0, 32), we get

32 = ab⁰ 

32 = a(1)

a = 32

Applying the value of a in (1), we get

y = 32b^x

Applying the point (1, 16), we get

16 = 32(b)¹

16/32 = b

b = 1/2

y = 32(1/2)^x