DESCRIBE THE TRANSFORMATION OF A SQUARE ROOT FUNCTION

Describe the transformations from the graph of f(x) = √x to the graph of h. Then graph h.

Problem 1 :

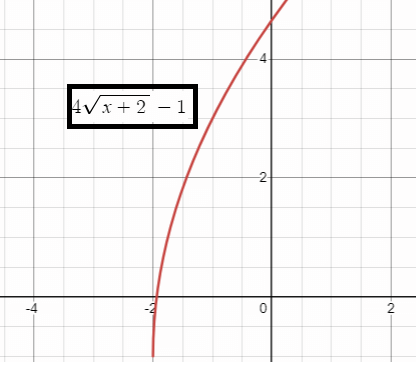
h(x) = 4√(x + 2) - 1

Solution :

h(x) = 4√(x + 2) - 1

Considering the function with y = a√b(x - h) + k

h(x) = 4√(x - (-2)) - 1

a = 4, h = -2 and k = -1

• a > 1, so it is vertical stretch of 4 units.
• h = -2, then horizontal move of 2 units to the left.
• k = -1, then vertical move of 1 unit to the down.

Problem 2 :

h(x) = (1/2)√(x - 6) + 3

Solution :

h(x) = (1/2)√(x - 6) + 3

Considering the function with y = a√b(x - h) + k

a = 1/2, h = 6 and k = 3

• 0 < a < 1, so it is vertical shrink of 1/2 units.
• h = 6, then horizontal move of 6 units to the right.
• k = 3, then vertical move of 3 units up.

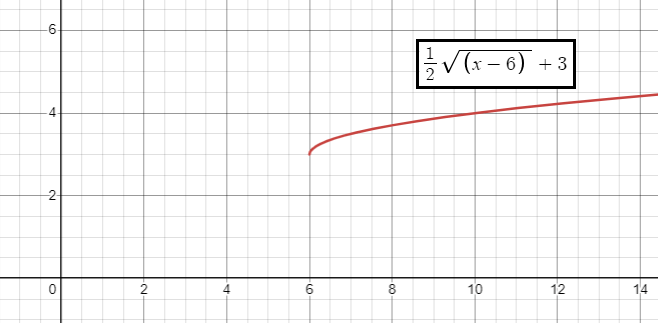
Problem 3 :

h(x) = (1/3)√(x + 3) - 3

Solution :

h(x) = (1/3)√(x + 3) - 3

h(x) = (1/3)√(x - (-3)) - 3

Considering the function with y = a√b(x - h) + k

a = 1/3, h = -3 and k = -3

• 0 < a < 1, so it is vertical shrink of 1/3 units.
• h = -3, then horizontal move of 3 units to the left.
• k = -3, then vertical move of 3 units down.

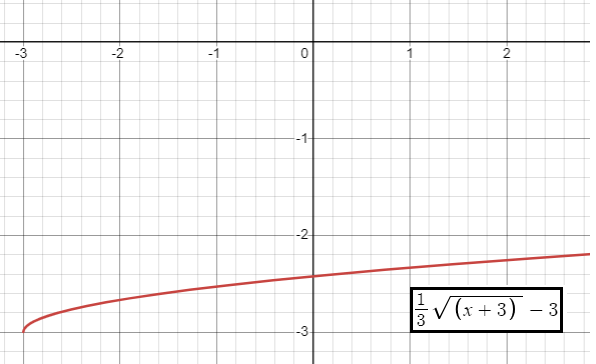
Problem 4 :

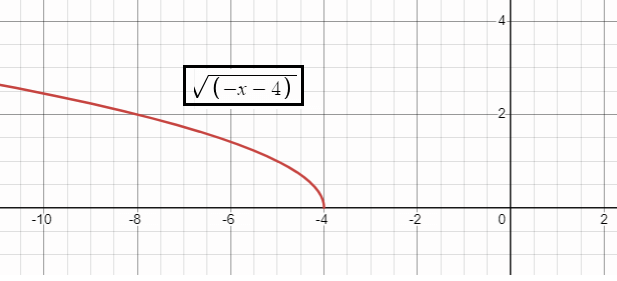
h(x) = √(-x - 4)

Solution :

h(x) = √(-x - 4)

h(x) = √-(x + 4)

h(x) = √-(x - (-4))

Considering the function with y = a√b(x - h) + k

b is negative , h = -4 and k = 0

• b is negative, so it is reflection across y-axis.
• h = -4, then horizontal move of 4 units to the left.
• k = 0, there is no vertical move.

Problem 5 :

How is the graph of y = √x - 5 translated from the graph of y = √x?

A. shifted 5 units left      B. shifted 5 units right

C. shifted 5 units up       D. shifted 5 units down

Solution :

y = √x - 5

Considering the function with y = a√b(x - h) + k

k = -5

So, the graph should be moved 5 units down. Option D is correct.

Problem 6 :

The parent function f(x) = √x is compressed vertically by a factor of 1/10, translated 4 units down, and reflected in the x-axis.

Solution :

Parent function :

f(x) = √x

Vertical compress with the factor of 1/10.

f(x) = (1/10) √x

Reflection about x-axis.

Put y = -y

f(x) = -(1/10) √x

Translating down 4 units, so k = -4

f(x) = -(1/10) √x - 4

So, the required function after the transformation is 

f(x) = -(1/10) √x - 4

Problem 7 :

The parent function f (x) = √x is compressed horizontally by a factor of 7.5 and translated 2 units up.

Solution :

Parent function :

f(x) = √x

Horizontal compression with the factor of 1/7.5 or 2/15

f(x) = √(2/15)x

Translation of 2 units up :

f(x) = √(2/15)x + 2

Problem 8 :

The parent function f(x) = √x is translated 1/2 unit left and stretched vertically by a factor of 3.

Solution :

Vertical stretch = 3 units

Translation of 1/2 units left

f(x) = 3√(x + 1/2)

Problem 9 :

The parent function f (x) = √x is stretched vertically by a factor of 10, translated 5 units down, and reflected in the y-axis.

Solution :

Vertical stretch = 10, a = 10

translating down = 5 units, k = -5

reflection across y-axis. Then x = -x

f(x) = 10√-x - 5