DESCARTES RULE OF SIGNS
It is known as Descartes’s Rule of Signs and this is how it works: If given a certain function with a polynomial that has real coefficients we’ll call f(x):
1) The number of positive real zeros of f(x) is either equal to the number of variations in sign of f(x) or is less than that number by an even integer.
2) The number of negative real zeros of f(x) is either equal to the number of variations in sign of f(-x) or is less than that number by an even integer
If p is the number of positive zeros of a polynomial P(x) will real coefficients and s is the number of sign changes in the coefficients of P(X), then s - p is a non negative even integer.
Non real roots :
Using the Descartes rule, we can compute a lower bound for the number of imaginary roots. Let m denote the number of sign changes in coefficients of P(x) of degree n;
let k denote the number of sign changes in coefficients of P(-x). Then there are at least n - (m + k) imaginary roots for the polynomial P(x).
Problem 1 :
Discuss the maximum possible number of positive and negative roots of the polynomial equation
9x9 - 4x8 + 4x7 - 3x6 + 2x5 + x3 + 7x2 + 7x + 2 = 0
Solution :
Let f(x) = 9x9 - 4x8 + 4x7 - 3x6 + 2x5 + x3 + 7x2 + 7x + 2
Number of roots (n) = 9
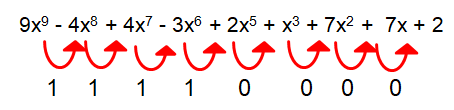
Total number of sign changes = 4
So, at least 4 positive real roots.
Here m = 4
f(-x) = -9x9 - 4x8 - 4x7 - 3x6 - 2x5 - x3 + 7x2 - 7x + 2
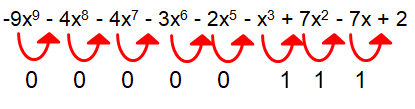
Total number of sign changes = 3
So, at least 3 negative real roots.
Here k = 3
Number of imaginary roots = n - (m + k)
= 9 - (4 + 3)
= 9 - 7
= 2
Then, 2 imaginary roots will be there.
Problem 2 :
Discuss the maximum possible number of positive and negative zeros of the polynomials
x2 - 5x + 6 and x2 - 5x + 16.
Also draw rough sketch of the graphs.
Solution :
Let p(x) = x2 - 5x + 6 and q(x) = x2 - 5x + 16.
Number of sign changes in p(x) = 2
Number of sign changes in q(-x) = 0
Number of sign changes in q(x) = 2
Number of sign changes in q(-x) = 0
Therefore it has atleast 2 positive roots and no negative roots.
Problem 3 :
Show that the equation
x9 - 5x5 + 4x4 + 2x2 + 1 = 0
has atleast 6 imaginary solutions.
Solution :
Let
p(x) = x9 - 5x5 + 4x4 + 2x2 + 1
+ - + + +
Number of sign changes in p(x) = 2
p(-x) = -x9 + 5x5 + 4x4 + 2x2 + 1
- + + + +
Number of sign changes in p(-x) = 1
n = 9, m = 2 and k = 1
Number of imaginary roots = 9 - (2 + 1)
= 9 - 3
= 6
So, it has atleast 6 imaginary roots.
Problem 4 :
Determine the number of positive and negative roots of the equation
x9 - 5x8 - 14x7 = 0
Solution :
Let p(x) = x9 - 5x8 - 14x7
Number of sign changes in p(x) = 1
p(-x) = -x9 - 5x8 + 14x7
Number of sign changes in p(-x) = 1
n = 9, m = 1 and k = 1
number of imaginary roots = 9 - (1 + 1)
= 9 - 2
= 7
number of imaginary roots = 7
So, the given polynomial will have atleast 1 positive root, 1 negative root and 7 imaginary roots.
Problem 5 :
Find the exact number of real zeros and imaginary of the polynomial
x9 + 9x7+ 7x5 + 5x3 + 3x
Solution :
p(x) = x9 + 9x7+ 7x5 + 5x3 + 3x
Number of sign changes in p(x) = 0
p(-x) = -x9 - 9x7- 7x5 - 5x3 - 3x
Number of sign changes in p(-x) = 0
n = 9, m = 0 and k = 0
number of imaginary roots = 9 - (0 + 0)
= 9 - 0
= 9
number of imaginary roots = 9
So, the given polynomial will have no positive, no negative and 9 imaginary roots.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling