DESCARTES RULE OF SIGNS EXAMPLES
It is known as Descartes’s Rule of Signs and this is how it works: If given a certain function with a polynomial that has real coefficients we’ll call f(x):
Number of positive roots :
1) The number of positive real zeros of f(x) is either equal to the number of variations in sign of f(x) or is less than that number by an even integer.
Number of negative roots :
2) The number of negative real zeros of f(x) is either equal to the number of variations in sign of f(-x) or is less than that number by an even integer
If p is the number of positive zeros of a polynomial P(x) will real coefficients and s is the number of sign changes in the coefficients of P(X), then s - p is a non negative even integer.
Non real roots :
Using the Descartes rule, we can compute a lower bound for the number of imaginary roots. Let m denote the number of sign changes in coefficients of P(x) of degree n;
let k denote the number of sign changes in coefficients of P(-x). Then there are at least n - (m + k) imaginary roots for the polynomial P(x).
State the possible number of positive and negative zeros for each function.
Problem 1 :
f(x) = 3x4 + 20x2 - 32
Solution:
Let f(x) = 3x4 + 20x2 - 32
Number of roots (n) = 4
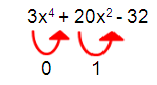
Total number of sign changes = 1
So, at least 1 positive real roots.
Here m = 1
f(-x) = 3(-x)4 + 20(-x)2 - 32
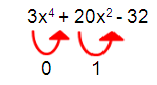
Total number of sign changes = 1
So, at least 1 negative real roots.
Here k = 1
Number of imaginary roots = n - (m + k)
= 4 - (1 + 1)
= 4 - 2
= 2
Then, 2 imaginary roots will be there.
Problem 2 :
f(x) = 5x4 - 42x2 + 49
Solution:
Let f(x) = 5x4 - 42x2 + 49
Number of roots (n) = 4
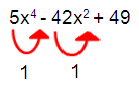
Total number of sign changes = 2
So, at least 2 positive real roots.
m = 2
f(-x) = 5x4 - 42x2 + 49
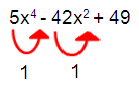
Total number of sign changes = 2
So, at least 2 negative real roots.
Here k = 2
Number of imaginary roots = n - (m + k)
= 4 - (2 + 2)
= 4 - 4
= 0
So, there is no imaginary roots.
Problem 3 :
f(x) = 4x3 - 12x2 - 5x + 1
Solution:
f(x) = 4x3 - 12x2 - 5x + 1
Number of sign changes in f(x) = 2
f(-x) = -4x3 - 12x2 + 5x + 1
Number of sign changes in f(-x) = 1
Problem 4 :
f(x) = 2x4 - 3x3 + x
Solution:
f(x) = 2x4 - 3x3 + x
Number of sign changes in f(x) = 2
f(-x) = 2x4 + 3x3 - x
Number of sign changes in f(-x) = 1
Problem 5 :
f(x) = 2x4 + 3x2 - 54
Solution:
f(x) = 2x4 + 3x2 - 54
Number of sign changes in f(x) = 1
f(-x) = 2x4 + 3x2 - 54
Number of sign changes in f(-x) = 1
n = 4, m = 1 and k = 1
number of imaginary roots = 4 - (1 + 1)
= 4 - 2
= 2
number of imaginary roots = 2
Problem 6 :
f(x) = x6 - 64
Solution:
f(x) = x6 - 64
Number of sign changes in f(x) = 1
f(-x) = x6 - 64
Number of sign changes in f(-x) = 1
n = 6, m = 1 and k = 1
number of imaginary roots = 6 - (1 + 1)
= 6 - 2
= 4
number of imaginary roots = 4
Problem 7 :
f(x) = 9x6 - 3x5 + 33x4 - 11x3 + 18x2 - 6x
Solution:
f(x) = 9x6 - 3x5 + 33x4 - 11x3 + 18x2 - 6x
Number of sign changes in f(x) = 5
f(-x) = 9x6 + 3x5 + 33x4 + 11x3 + 18x2 + 6x
Number of sign changes in f(-x) = 0
Problem 8 :
f(x) = 64x6 - 1
Solution:
f(x) = 64x6 - 1
Number of sign changes in f(x) = 1
f(-x) = 64x6 - 1
Number of sign changes in f(-x) = 1
n = 6, m = 1 and k = 1
number of imaginary roots = 6 - (1 + 1)
= 6 - 2
= 4
number of imaginary roots = 4
Problem 9 :
f(x) = 2x5 + 4x4 + 9x3 + 18x2 - 35x - 70
Solution:
f(x) = 2x5 + 4x4 + 9x3 + 18x2 - 35x - 70
Number of sign changes in f(x) = 1
f(-x) = -2x5 + 4x4 - 9x3 + 18x2 + 35x - 70
Number of sign changes in f(-x) = 4
Problem 10 :
f(x) = 6x5 - 4x4 - 63x3 + 42x2 + 147x - 98
Solution:
f(x) = 6x5 - 4x4 - 63x3 + 42x2 + 147x - 98
Number of sign changes in f(x) = 3
f(-x) = -6x5 - 4x4 + 63x3 + 42x2 - 147x - 98
Number of sign changes in f(-x) = 2
Problem 11 :
f(x) = 16x6 - 32x4 - 25x2 + 50
Solution:
f(x) = 16x6 - 32x4 - 25x2 + 50
Number of sign changes in f(x) = 2
f(-x) = 16x6 - 32x4 - 25x2 + 50
Number of sign changes in f(-x) = 2
n = 6, m = 2 and k = 2
number of imaginary roots = 6 - (2 + 2)
= 6 - 4
= 2
number of imaginary roots = 2
Problem 12 :
f(x) = x7 - 64x
Solution:
f(x) = x7 - 64x
Number of sign changes in f(x) = 1
f(-x) = -x7 + 64x
Number of sign changes in f(-x) = 1
n = 7, m = 1 and k = 1
number of imaginary roots = 7 - (1 + 1)
= 7 - 2
= 5
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling