DEFINITIONS  AND POSTULATES IN GEOMETRY

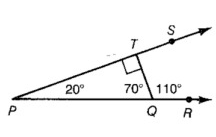
Refer to the diagram and name each of the following.

Problem 1 :

An angle adjacent to ∠PQT _____

Solution :

Adjacent angle :

Two angles are adjacent if they have a common vertex and a common side.

In the diagram, the two angles PQT and TQR are adjacent.

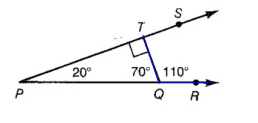
Problem 2 :

The ray opposite to the ray TS _____

Solution :

Opposite rays :

Two rays are opposite rays, by definition, if 

1) They have the same endpoint, and 

2) Their union is a line.

In the diagram, opposite ray is QR or PR.

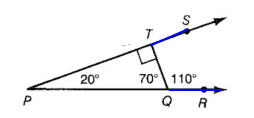
Problem 3 :

An obtuse angle _____

Solution :

An angle that is greater than 90^º and less than 180^º is called obtuse angle.

Problem 4 :

The sides of ∠TQR ____ and _____

Solution :

So, the sides is ∠TQP  are TQ and QR.

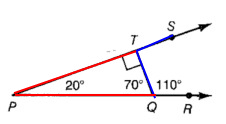
Problem 5 :

Two right angles _____ and ____

Solution :

Two right angles measures is 90^º and 90^º

So, two right triangle is ∠PTQ and ∠STQ

Problem 6 :

A point on the line PQ that is not on line segment PQ _____

Solution :

R is the point of PQ which is not in the line segment PQ.

Problem 7 :

The vertex of the 20^º angle _____

Solution :

The vertex of the 20^º angle is P.

Problem 8 :

The point between P and R _____

Solution :

The point between P and R is Q.

Classify each statement as true or false.

Problem 1 :

Through any two points there is exactly one line. _____

Solution :

Yes, it is true. Because exactly one line to pass through two points.

Problem 2 :

Through any three points there is exactly one line. _____

Solution :

Yes, it is true. A line can be drawn by connecting infinite points, so any three points can be on the line.

Problem 3 :

Through any three points there is exactly one plane. _____

Solution :

It is false. Because through any three non - collinear points, there exists exactly one plane.

Problem 4 :

Two lines intersect in exactly one point. _____

Solution :

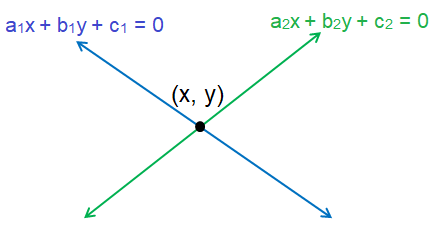
Yes, it is true.

Problem 5 :

Two planes intersect in exactly one point. _____

Solution :

It is false. Because planes are infinite.

Problem 6 :

Two planes intersect in a line. _____

Solution :

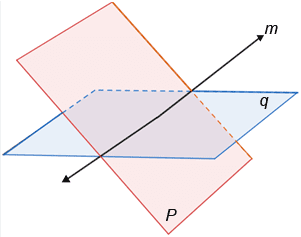
Yes it is true. If two planes intersect, then their intersection is a line.

Problem 7 :

A line and a plane can intersect in a point. _____

Solution :

A line and plane can intersect at a point, sometime infinitely many points.

So, it is true.

Complete each statement with the word always, sometimes, or never.

Problem 1 :

Adjacent angles are _____ congruent.

Solution :

Adjacent angles are sometimes congruent. The equivalent angle measure would be 90 degree.

Adjacent angles are angles that come out of the same vertex.

Problem 2 :

If points A and B are in plane R and point C is on AB, then C is _____ in R.

Solution :

If points A and B are in plane R and point C is on AB, then C is always in R.

Problem 3 :

Two intersecting lines _____ lie in exactly one plane.

Solution :

Two intersecting lines always lie in exactly one plane.

Problem 4 :

A line and a point not on the line _____ lie in more than one plane.

Solution :

A line and a point not on the line never lie in more than one plane.

Problem 5 :

A line _____ contains at least two points.

Solution :

A line always contains at least two points.