COUNT HOW MANY TIMES THE ELEMENT IS REPEATING

Problem 1 :

The first 40 odd counting numbers are written. How many times does ‘3’ appear as a digit?

Solution :

Writing 40 odd numbers, each row contains 10 numbers each

Row 1 ==> 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 

Row 2 ==> 21, 23, 25, 27, 29, 31, 33, 35, 37, 39,

Row 3 ==> 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 

Row 4 ==> 61, 63, 65, 67, 69, 71, 73, 75, 77, 79

Total number of 3's in first 40 numbers = 13.

Problem 2 :

Anna writes down all numbers from 1 to 100. How many times did she write the digit 2?

(A) 18     (B) 19     (C) 20     (D) 21     (E) 22

Solution :

Writing down numbers from 1 to 100, each row consists of 10 numbers.

1, 2, 3, 4, 5, 6, 7, 8, 9, 10

11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ........ 100

= 1+2+10+1+1+1+1+1+1+1

= 13 + 7(1)

= 20

So, we have 20 two's.

Problem 3 :

Alice types the fraction 30/37 into an online calculator and it calculates the decimal form to thousands of decimal places. What is the sum of the first 2020 digits after the decimal?

(A) 6060    (B) 6061     (C) 6062    (D) 6063 (E) 6064 (F) 6065

Solution :

30/37 = 0.810 810 .........

Here 3 digits is repeating (8, 1, 0).

Here we should find the sum of first 2020 digits after the decimal.

Now, let us find the number of groups in 2020 digits so each group consist of 3 digits.

2020/3 ==> 3 (673) + 1

Sum of the digits in each group is 9.

So, sum of all 673 groups will be 9(673), that is 6057

So far, we got sum of 2016 digits, this sum to be added with 2020 th digit that is 8.

6057 + 8 ==> 6065

So, the answer is 6065.

Problem 4 :

Grace chooses 5 different numbers from the list 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Two of those numbers are 4 and 5, and they are only two numbers she picks that differ by 1. What is the greatest possible sum of five numbers ?

Solution :

In the five numbers she is choosing 4 and 5 are numbers which has the difference 1.

In order to get the sum as greatest possible number, we should choose 10.

If she chooses 10, we cannot choose 9. She can choose 8. So, the numbers she is choosing sofar are, 10, 8, 5 and 4

The remaining 1 number will be 2. The sum of the numbers

= 10 + 8 + 5 + 4 + 2

= 29

So, the required greatest possible sum is 29.

Problem 5 :

In the pattern below, what will be the 78th letter written? ABBCCDABBCCD… ( and so on)

Solution :

In the given written as pattern, there is a rule

A = 1's, B = twice, C = twice, D = 1's 

Each group will consist of 1+2+2+1, that is 6 variables.

To get the variable we have is 78^th position, let us divide 78 by 6.

13 groups will be there and 78 is the last element of the group. So, the required answer is D.

Problem 6 :

What is the sum of the digits in the arrangement given below ?

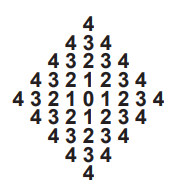
Solution :

Starting from the middle row, we have 9 rows.

Number of 4's = 1 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 1

= 16(4)

= 64

Number of 3's = 0 + 1 + 2 + 2 + 2 + 2 + 2 + 1 + 0

= 12(3)

= 36

Number of 2's = 0 + 0 + 1 + 2 + 2 + 2 + 1 + 0 + 0

= 8(2)

= 16

Number of 1's = 0 + 0 + 0 + 1 + 2 + 1 + 0 + 0 + 0

= 4(1)

= 4

Sum of the values = 64 + 36 + 16 + 4

= 120