COSINE LAW WORD PROBLEMS

The cosine law can be used which is not a right triangle.

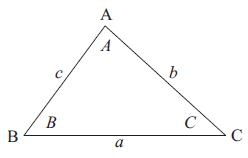
a² = b² + c² - 2bc cos A

b² = c² + a² - 2ac cos B

c² = a² + b² - 2ab cos C

Problem 1 :

Calculate the perimeter of triangle ABC.

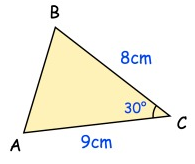
Solution:

By using cosine rule,

a² = b² + c² - 2bc cos(A)

a² = 8² + 9² - 2(8)(9) cos(30°)

a² = 64 + 81 - 72(√3)

a² = 145 - 124.7

a² = 20.29

a = √20.29

a = 4.5 cm

Perimeter = a + b + c

= 4.5 + 8 + 9

= 21.5 cm

So, the perimeter of triangle ABC is 21.5 cm.

Problem 2 :

Boat A is 16 km from a lighthouse on a bearing of 055°. Boat B is 11 km from the same lighthouse on a bearing of 152°. Calculate the distance between the two boats.

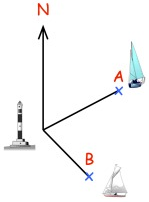
Solution:

∠BLA = 152° - 55°

= 87°

By using cosine law,

AB² = LA² + LB² - 2(LA)(LB) Cos ∠BLA

= 16² + 11² - 2(16)(11) Cos (87°)

= 256 + 121 - 352(0.052)

= 377 - 18.42

AB² = 358.58

AB = √358.58

= 18.94 km

So, the distance between the two boat is 18.94 km.

Problem 3 :

Shown is sector OAB.

O is the centre of the circle with radius 9 cm.

A and B are points on the circle.

The length of the chord AB is 10.35 cm.

Find the area of sector OAB.

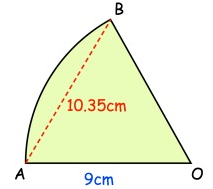
Solution:

Given, OA = 9 cm, OB = 9 cm and AB = 10.35 cm

By using cosine law,

Problem 4 :

A hot air balloon is flying above two point, standing on the ground at points A and B, 600m apart.

The hot air balloon is 300 m from A and 500 m from B.

(a) Work out the angle of elevation from point B.

(b) How high is the hot air balloon from the ground?

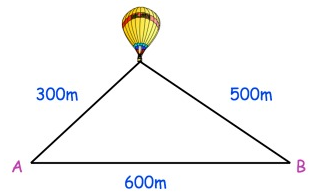
Solution:

a) 

500² - x² = 300² - (600 - x)²

250000 - x² = 90000 - x² + 1200x - 360000

1200x = 520000

b.

Problem 5 :

A boat, located at position X is running out of fuel.

There are two ports located at Y and Z.

The boat must refuel as soon as possible.

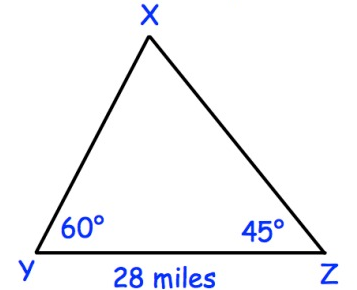
How much closer is the boat to the port at Y than the port at Z?

Solution:

angle x is equal to 180° - 60° - 45° = 75°

Using the law of sine,

y - z = 25.12 - 20.5

= 4.62 miles 

The distance is 4.62 miles.

From X to Z is 4.62 miles closer then X to Y.