CONVERTING RECURSIVE AND EXPLICIT FORMS OF SEQUENCE

Given the recursive formula, write the explicit formula for the sequence.

Problem 1 :

t₁ = 0

t_n = t_n-1 + 6

Solution :

t_n = t_n-1 + 6

n = 2 substitute the given equation.

t₂ = t_2-1 + 6

t₂ = t₁ + 6

Given t₁ = 0

t₂ = 0 + 6

t₂ = 6

0, 6, ...

Explicit formula :

t_n = a + (n - 1)d

d = t₂ - t₁

= 6 - 0

= 6

t_n = a + (n - 1)6

t_n = a + (n - 1)6

t_n = 6n - 6

Problem 2 :

t₁ = -4

t_n = t_{n - 1} + 2

Solution :

t_n = t_n-1 + 2

n = 2 ... substitute the given equation.

t₂ = t_2-1 + 2

t₂ = t₁ + 2

Given t₁ = -4

t₂ = -4 + 2

t₂ = -2

-4, -2,  ...

Explicit formula :

t_n = t + (n - 1)d

d = t₂ -t₁

= -2 - (-4)

= -2 + 4

= 2

t_n = -4 + (n - 1)2

= -4 + 2n - 2

t_n = 2n - 6

Problem 3 :

t₁ = 8

t_n = t_n-1 - 4

Solution :

t_n = t_n-1 - 4

n = 2,  ... substitute the given equation.

t₂ = t_2-1 - 4

t₂ = t₁ - 4

Given t₁ = 8

t₂ = 8 - 4

t₂ = 4

8, 4, ...

Explicit formula :

t_n = t + (n - 1)d

d = t₂ - t₁

= 4 - 8

= -4

t_n = 8 + (n - 1)(-4)

= 8 - 4n + 4

t_n = 12 - 4n

Given the explicit formula, write the recursive formula for the sequence.

Problem 1 :

t_n = 3n - 1

Solution :

t_n = 3n - 1

n = 1, 2,   ... substitute the given equation.

2, 5, ...

Recursive formula :

t_n = t_{n - 1} + d

d = t₂ - t₁

= 5 - 2

= 3

t_n = t_{n - 1} + 3

Problem 2 :

t_n = 4n + 3

Solution :

t_n = 4n + 3

n = 1, 2,   ... substitute the given equation.

7, 11, ...

Recursive formula :

t_n = t_{n - 1} + d

d = t₂ - t₁

= 11 - 7

= 4

t_n = t_{n - 1} + 4

Problem 3 :

t_n = -5n + 2

Solution :

t_n = -5n + 2

n = 1, 2,   ... substitute the given equation.

-3, -8, ...

Recursive formula :

t_n = t_{n - 1} + d

d = t₂ - t₁

= -8 - (-3)

= -8 + 3

= -5

t_n = t_{n - 1} - 5

Problem 4 :

Given the recursive formula

f(n) = f(n - 1) + 3

f(1) = -5

a) Find the first four terms of the sequence.

b) Rewrite those four terms as order pairs and graph the sequence.

c) Find an explicit formula for the sequence.

d) Find the value of the 30^th term of the sequence. Which formula is more efficient for this question the recursive formula or the explicit formula ? Explain your answer.

Solution :

a) To find first four terms of the sequence :

f(n) = f(n - 1) + 3

f(1) = -5

Hence, the first four terms of the sequence is -5, -2, 1 and 4.

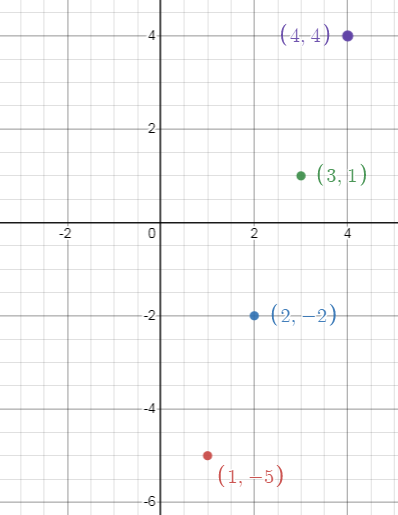
b) Order pairs and graph the sequence :

(1, -5), (2, -2), (3, 1), (4, 4)

c) 

Explicit formula :

a_n = a + (n - 1)d

a_n = -5 + (n - 1)3

 = -5 + 3n - 3

a_n = 3n - 8

d)

Explicit formula :

a₃₀ = 3(30) - 8

a₃₀ = 82

Recursive formula :

a_n = a_{n - 1} + d

a₃₀ = a₂₉+ 3

The explicit formula is more efficient because it allows us to find the value of the 30th term directly.