CONVERTING BETWEEN RADICAL FORM AND EXPONENT FORM

To convert the radical to exponential form, we follow the rules given below.

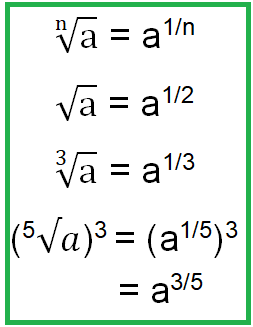
Writing expressions in rational exponential form :

Problem 1 :

(√5)³

Solution :

Since it is square root, we have to write 1/2 as exponent.

When we have power raised to another power, we can multiply the powers.

= (5³)^1/2

= 5^{3 x (1/2)}

= 5^(3/2)

Problem 2 :

(∜4)²

Solution :

Since it is fourth root, we have to write 1/4 as exponent. 

When we have power raised to another power, we can multiply the powers.

= (∜4)²

= (4^1/4)²

= 4^{(1/4) x 2}

= 4^(1/2)

Wrting 4 in expanded form, we get

4 = 2 x 2

= 2^2(1/2)

= 2^{2 x 1/2}

= 2

Problem 3 :

(∛9)²

Solution :

= (∛9)²

= (9^1/3)²

= 9^2/3

Writing 9 in expanded form, we get

9 = 3 x 3

= (3²)^2/3

= 3^{2 x (2/3)}

= 3^{2 x (2/3)}

= 3^4/3

Problem 4 :

(5^th root of 10)⁴

Solution :

= (5^th root of 10)⁴

= [(10)^1/5]⁴

= 10^4/5

Problem 5 :

(√15)³

Solution :

= (√15)³

= [(15)^1/2]³

= (15)^3/2

Problem 6 :

(∛27)⁴

Solution :

= (∛27)⁴

27 = 3 x 3 x 3

(∛27)⁴ = (3³)⁴

= 3^3x4

= 3¹²

Simplify the following :

Problem 7 :

(∛x ⋅ √x⁵) / √25x¹⁶

Solution :

= (∛x ⋅ √x⁵) / √25x¹⁶

= (x^1/3 ⋅ (x⁵)^1/2) / √(5 ⋅ 5 ⋅ x⁸ ⋅ x⁸)

= (x^{1/3 + 5/2}) / 5 ⋅ x⁸

= x^17/6 / 5 ⋅ x⁸

= (1/5) x^{(17/6) - 8}

= (1/5) x^{(17 - 48)/6}

= (1/5) x^-31/6

= (1/5 x^31/6)

Problem 8 :

∜(81x⁵ y² z⁸)

Solution :

= ∜(81x⁵ y² z⁸)

= (81x⁵ y² z⁸)^1/4

= (3⁴ x⁵ y² z⁸)^1/4

= (3⁴)^1/4 (x⁵ y² z⁸)^1/4

= 3x  x^1/4 y^{2 x (1/4)} z^{8 x 1/4}

= 3x x^1/4 y^(1/2) z²

= 3x  z² ∜x √y

Solve the equation :

Problem 8 :

(a) 4x⁵ = 128

(b) (x − 3)⁴ = 21

Solution :

(a) 4x⁵ = 128

x⁵ = 128/4

x⁵ = 32

32 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2

x⁵ = 2⁵

Since the powers are equal, then we can equate the bases.

x = 2

(b) (x − 3)⁴ = 21

x - 3 = ∜21

x - 3 = 2.14

x = 2.14 + 3

x = 5.14

evaluate the expression using a calculator. Round your answer to two decimal places when appropriate.

Problem 9 :

5^th root (32768)

Solution :

= 5^th root (32768)

Writing 32768 in expanded form, we get

32768 = 2¹⁵

5^th root (32768) = (2¹⁵)^1/5

= 2^{15 x (1/5)}

= 2³

= 8

Problem 10 :

343 = (4r + 1)³

Solution :

343 = (4r + 1)³

(4r + 1)³ = 343

4r + 1 = ∛343

4r + 1 = ∛7 x 7 x 7

4r + 1 = 7

4r = 7 - 1

4r = 6

r = 6/4

r = 3/2

So, the value of r is 3/2.

Problem 11 :

-8x⁴ = -128

Solution :

-8x⁴ = -128

x⁴ = 128/8

x⁴ = 32/2

x⁴ = 16

16 = 2 ⋅ 2 ⋅ 2 ⋅ 2

16 = 2⁴

x⁴ = 2⁴

x = 2

Problem 12 :

Your friend claims it is not possible to simplify the expression 7 √11 − 9 √44 because it does not contain like radicals. Is your friend correct? Explain your reasoning.

Solution :

= 7 √11 − 9 √44

= 7 √11 − 9 √(2 ⋅ 2 ⋅ 11)

= 7 √11 − (9 ⋅ 2)√11

= 7 √11 − 18√11

= - 9√11

It can be simplified. So your friend claim is incorrect.

Problem 13 :

Evaluate :

i)  (0.000064)^5/6

ii)  [(625^-1/2)^-1/4]²

iii)  (512)^-2/9

iv)  [(216)^2/3]^1/2

Solution :

i)  (0.000064)^5/6

0.0000064 =  64/1000000

64 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ==> 2⁵

1000000 = 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10==> 10⁶

(0.000064)^5/6 = (2⁶/10⁶)^5/6

= [(2/10)⁶]^5/6

= (2/10)^6x(5/6)

= (2/10)⁵

= (2⁵/10⁵)

= 32/100000

= 0.00032

ii)  [(625^-1/2)^-1/4]²

625 = 5 ⋅ 5 ⋅ 5 ⋅ 5 ==> 5⁴

[(625^-1/2)^-1/4]² = [(5⁴)^-1/2)^-1/4]²

= [(5⁴)^-1/8]²

= (5⁴)^-1/4

= 5^-1

= 1/5

iii)  (512)^-2/9

512 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2

= 2⁶

 (512)^-2/9 = (2⁶)^-2/9

= (2²)^-2/3

= 2^-4/3

= 1/2^4/3

= 1/∛2⁴

= 1/2∛2

iv)  [(216)^2/3]^1/2

216 = 6 x 6 x 6

= 6³

[(216)^2/3]^1/2 = [ (6³))^2/3]^1/2

=  [ (6²)²]^1/2

=  [ (6⁴]^1/2

=  6²

= 36

Problem 14 :

Write each expression in radical form.

a) (6n)^1/2

b) (5n)^5/3

c) (7m)^-5/2

d) (7b)^2/3

Solution :

a) (6n)^1/2

Power 1/2 and square root both are the same.

= √6n

b) (5n)^5/3

5/3 can be written as 5 x 1/3. Here 1/3 can be converted into cube root and 5 can be kept as exponent.

=  ∛(5n)⁵

c) (7m)^-5/2

= 1/(7m)^5/2

5/2 can be written as 5 x 1/2. Here 1/2 can be converted into square root and 5 will be kept as exponent.

= 1/√(7m)⁵

d) (7b)^2/3

2/3 can be written as 2 x 1/3. Here 1/3 can be written as cube root and 2 can be kept in the power.

= √(7b)⁵