CONVERT INEQUALITIES TO INTERVAL NOTATION

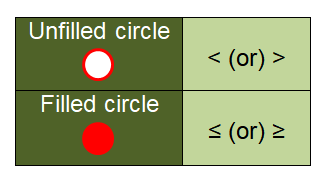
How to plot inequality on the number line ?

• If we have the inequality

< (less than) or > (greater than),

we have to use the empty / unfilled circle.

• If we have the inequality sign 

≤ (less than or equal to) or ≥ (greater than or equal to),

we have to use the filled circle.

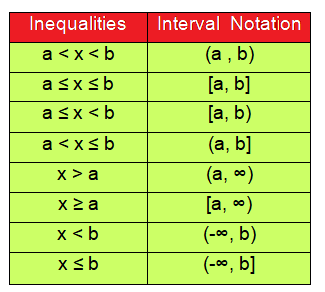
To convert inequalities into interval notation, we need to know the table below.

Write these number sets using interval notation :

Example 1 :

{x│-1 ≤ x ≤ 6}

Solution :

-1 ≤ x ≤ 6

Here, we are having the both side signs ≤ (less than or equal to). So we have to use filled circle.

Hence, the required interval notation is [1, 6].

Example 2 :

{x│ 0 < x < 5}

Solution:

0 < x < 5

Here, we are having the both side signs < (less than). So have to use unfilled circle.

Hence, the required interval notation is (0, 5).

Example 3 :

{x│-4 < x ≤ 7}

Solution :

-4 < x ≤ 7

Here, we are having the both side signs < and ≤ (less than and less than or equal to). So have to use filled circle and unfilled circle.

Hence, the required interval notation is (-4, 7].

Example 4 :

{x│ 4 ≤ x < 8}

Solution :

4 ≤ x < 8

Here, we are having the both side signs < and ≤ (less than and less than or equal to). So have to use filled circle and unfilled circle.

Hence, the required interval notation is [4, 8).

Example 5 :

{x│ x ≤ 2 or x ≥ 5}

Solution :

Here, both inequalities are having the sign ≤ or ≥. So we have to use filled circle.

Since we have OR, we combine all the solution of both inequalities.

Hence, the required interval notation is (-∞,2] υ [5, ∞)

Example 6 :

 {x│ x < -3 or x > 4}

Solution :

Here, both inequalities are having the sign < or >. So we have to use unfilled circle.

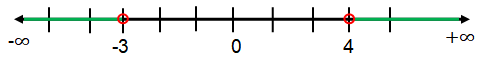
Hence, the required interval notation is (-∞, 3) υ (4, ∞).

Example 7 :

 {x│ -1 < x ≤ 1 or x ≥ 2}

Solution :

Hence, the required interval notation is (-1, 1] υ [2, ∞)

Example 8 :

 {x│ x < -4 or 2 ≤ x < 7}

Solution :

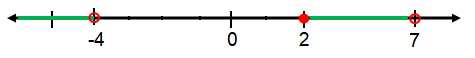
Hence, the required interval notation is (-∞, 4) υ [2, 7).

Example 9 :

Write each sentence as an inequality and interval notation.

a. A number w minus 3.5 is less than or equal to −2.

b. Three is less than a number n plus 5.

c. Zero is greater than or equal to twice a number x plus 1.

Solution :

a. Let w be the required number.

w - 3.5 ≤ -2

Solving for w, we get

w ≤ -2 + 3.5

w ≤ 1.5

Converting into interval notation :

(-∞, 1.5]

b. Let n be the number.

Number plus 5, then n + 5

Three is less than a number n plus 5.

3 < n + 5

Solving for n, we get

3 - 5 < n

-2 < n

Converting into interval notation :

(-2, ∞)

c. Let x be the number.

0 > 2x + 1

-1 > 2x

Solving for x,

-1/2 > x

Converting into interval notation :

(-∞, -1/2)

Example 10 :

The graphs show the height restrictions h (in inches) for two rides at an amusement park. Write an inequality that represents the height restriction of each ride.

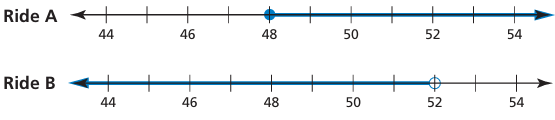
Solution :

Converting each number line into interval notation, we get

For ride A :

[48, ∞)

For ride B :

(-∞, 52)

Common solution for both intervals is, 

So, h ≥ 48 represents the height restriction for Ride A, and h < 52 represents the height restriction for Ride B

Example 11   :

Write the sentence as an inequality.

1)  A number x is greater than 3.

2)  A number n plus 7 is less than or equal to 9.

3) Fifteen is no more than a number t divided by 5.

4) Three times a number w is less than 18.

5) One-half of a number y is more than 22.

6) Three is less than the sum of a number s and 4.

7) Thirteen is at least the difference of a number v and 1.

8)  Four is no less than the quotient of a number x and 2.1

Solution :

1) x is greater than 3, x > 3

2) Let n be the number.

n + 7 ≤ 9

Solving for n, we get

n ≤ 9 - 7

n ≤ 2

3) 15 < t/5

Solving for t, we get

15(5) < t

75 < t

4) 3w < 18

Solving for w, we get

w < 18/3

w < 6

5) (1/2) of y > 22 

Solving for y, we get

(1/2)y > 22

y > 22(2)

y > 44

6) 3 < s + 4

Solving for s, we get

3 - 4 < s

-1 < s

7) 13 > v + 1

Solving for v, we get

13 - 1 > v

12 > v

8)  4 < x/2.1

Solving for x, we get

4(2.1) < x

8.4 < x