CONVERT FROM GENERAL FORM TO STANDARD FORM OF A CIRCLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Write each of the following in standard form. Identify the center of the circle as well as the length of the radius, the graph the circle if possible.
Problem 1 :
x2 + y2 + 10x - 4y + 13 = 0
Solution :
x2 + y2 + 10x - 4y + 13 = 0
Write x - terms and y - terms together.
x2 + 10x + y2 - 4y + 13 = 0
Completing the square.
x2 + 10x + 52 - 52 + y2 - 4y + 22 - 22 + 13 = 0
(x + 5)2 - 52 + (y - 2)2 - 22 + 13 = 0
(x + 5)2 - 25 + (y - 2)2 - 4 + 13 = 0
(x + 5)2 + (y - 2)2 - 16 = 0
Add 16 to each side.
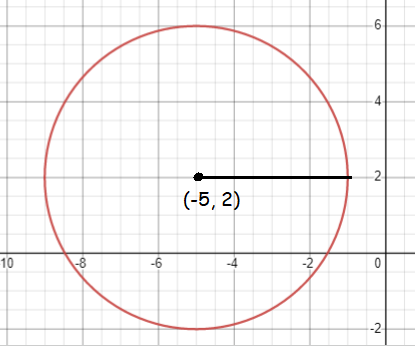
(x + 5)2 + (y - 2)2 = 16
(x + 5)2 + (y - 2)2 = 42
The above equation of the circle is in standard form.
Center (h, k) = (-5, 2)
Radius = 4
Problem 2 :
x2 + y2 + 6y - 16 = 0
Solution :
x2 + y2 + 6y - 16 = 0
Write x - terms and y - terms together.
x2 + y2 + 6y - 16 = 0
Completing the square.
x2 + y2 + 6y + 32 - 32 - 16 = 0
x2 + (y + 3)2 - 32 - 16 = 0
x2 + (y + 3)2 - 9 - 16 = 0
x2 + (y + 3)2 - 25 = 0
Add 25 on each sides.
x2 + (y + 3)2 = 25
x2 + (y + 3)2 = 52
The above equation of the circle is in standard form.
Center (h, k) = (0, -3)
Radius = 5
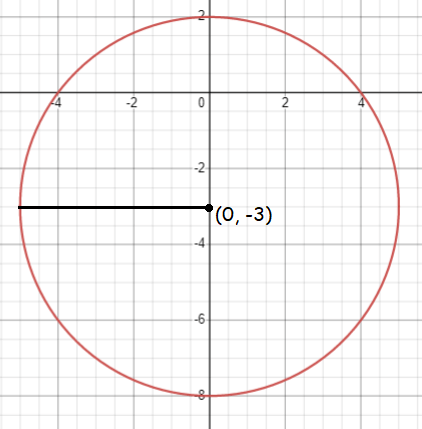
Problem 3 :
x2 + y2 - 4x - 8y + 11 = 0
Solution :
x2 + y2 - 4x - 8y + 11 = 0
Write x - terms and y - terms together.
x2 - 4x + y2 - 8y + 11 = 0
Completing the square.
x2 - 4x + 22 - 22 + y2 - 8y + 42 - 42 + 11 = 0
(x - 2)2 - 22 + (y - 4)2 - 42 + 11 = 0
(x - 2)2 - 4 + (y - 4)2 - 16 + 11 = 0
(x - 2)2 + (y - 4)2 - 9 = 0
Add 9 to each side.
(x - 2)2 + (y - 4)2 = 9
(x - 2)2 + (y - 4)2 = 32
The above equation of the circle is in standard form.
Center (h, k) = (2, 4)
Radius = 3
Problem 4 :
x2 + y2 + 6x - 8y + 29 = 0
Solution :
x2 + y2 + 6x - 8y + 29 = 0
Write x - terms and y - terms together.
x2 + 6x + y2 - 8y + 29 = 0
Completing the square.
x2 + 6x + 32 - 32 + y2 - 8y + 42 - 42 + 29 = 0
(x + 3)2 - 32 + (y - 4)2 - 42 + 29 = 0
(x + 3)2 - 9 + (y - 4)2 - 16 + 29 = 0
(x + 3)2 + (y - 4)2 + 4 = 0
Subtract 4 on each sides.
(x + 3)2 + (y - 4)2 = -4
There is no circle.
Problem 5 :
x2 + y2 - 8x - 20 = 0
Solution :
x2 + y2 - 8x - 20 = 0
Write x - terms and y - terms together.
x2 - 8x + y2 - 20 = 0
Completing the square.
x2 - 8x + 42 - 42 + y2 - 20 = 0
(x - 4)2 - 42 + y2 - 20 = 0
(x - 4)2 - 16 + y2 - 20 = 0
(x - 4)2 + y2 - 36 = 0
Add 36 to each sides.
(x - 4)2 + y2 = 36
(x - 4)2 + y2 = 6
The above equation of the circle is in standard form.
Center (h, k) = (4, 0)
Radius = 6
Problem 6 :
2x2 + 2y2 + 4x - 12y + 2 = 0
Solution :
2x2 + 2y2 + 4x - 12y + 2 = 0
2(x2 + y2 + 2x - 6y + 1) = 0
Dividing 2 on each sides.
x2 + y2 + 2x - 6y + 1 = 0
Write x - terms and y - terms together.
x2 + 2x + y2 - 6y + 1 = 0
Completing the square.
x2 + 2x + 12 - 12 + y2 - 6y + 32 - 32 + 1 = 0
(x + 1)2 - 12 + (y - 3)2 - 32 + 1 = 0
(x + 1)2 - 1 + (y - 3)2 - 9 + 1 = 0
(x + 1)2 + (y - 3)2 - 9 = 0
Add 9 to each side.
(x + 1)2 + (y - 3)2 = 9
(x + 1)2 + (y - 3)2 = 32
The above equation of the circle is in standard form.
Center (h, k) = (-1, 3)
Radius = 3
Problem 7 :
3x2 + 3y2 + 36x + 30y + 171 = 0
Solution :
3x2 + 3y2 + 36x + 30y + 171 = 0
3(x2 + y2 + 12x + 10y + 57) = 0
Dividing 3 on each sides.
x2 + y2 + 12x + 10y + 57 = 0
Write x - terms and y - terms together.
x2 + 12x + y2 + 10y + 57 = 0
Completing the square.
x2 + 12x + 62 - 62 + y2 + 10y + 52 - 52 + 57 = 0
(x + 6)2 - 62 + (y + 5)2 - 52 + 57 = 0
(x + 6)2 - 36 + (y + 5)2 - 25 + 57 = 0
(x + 6)2 + (y + 5)2 - 4 = 0
Add 4 to each sides.
(x + 6)2 + (y + 5)2 = 4
(x + 6)2 + (y + 5)2 = 22
The above equation of the circle is in standard form.
Center (h, k) = (-6, -5)
Radius = 2
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling