CONVERT BETWEEN SCIENTIFIC NOTATION AND STANDARD FORM

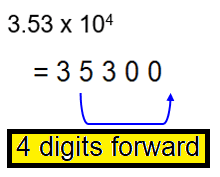
Scientific notation helps us to represent the numbers which are very huge or very tiny in a form of multiplication of single-digit numbers and 10 raised to the power of the respective exponent.

• The exponent is positive if the number is very large.
• It is negative if the number is very small.

a × 10^b ; 1 ≤ a < 10

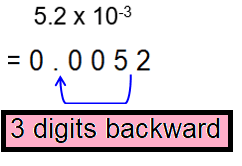Convert Between Scientific Notation and Standard Form

Problem 1 :

5.3 × 10⁶

Solution :

Exponent is positive, so we have to move the decimal 6 digits to the right.

But we have one digit after the decimal.  We should use zeroes for the rest of the places.

5300000.

So, the number 5.3 × 10⁶ in standard notation is 53,00,000.

Problem 2 :

4.7 × 10^-5

Solution :

= 4.7 × 10^-5

Exponent is negative, so we have to move the decimal 5 digits to the left.

= 0.000047

Problem 3 :

5 × 10⁴

Solution :

= 5 × 10⁴

Exponent is positive, so we have to move the decimal 4 digits to the right.

50000.

So, the number  5 × 10⁴ in standard notation  is 50000.

Problem 4 :

4.59 × 10¹

Solution :

= 4.59 × 10¹

Exponent is positive 1, so we have to move the decimal one digit to the right.

= 45.9

So, the number  4.59 × 10¹ in standard notation is 45.9.

Problem 5 :

6.7 × 10⁴

Solution :

= 6.7 × 10⁴

We have positive 4, so move the decimal 4 digits to the right.

So, the number  6.7 × 10⁴ in standard notation is 67000.

Problem 6 :

9.6 × 10⁴

Solution :

= 9.6 × 10⁴

We have positive 4, so move the decimal 4 digits to the right.

= 96000

Problem 7 :

8.78 × 10³

Solution :

= 8.78 × 10³

Exponent is positive 3, so we have to move the decimal 3 digits to the right.

8780.

Problem 8 :

5.82 × 10³

Solution :

= 5.82 × 10³

We have positive exponent, we have to move the decimal to the right.

= 5820

So, the number  5.82 × 10³ in standard notation is 5820.

Problem 9 :

1.3 × 10⁵

Solution :

= 1.3 × 10⁵

We have positive exponent, so we have to move the decimal 5 digits to the right.

= 130000

Problem 10 :

4.1 × 10⁴

Solution :

= 4.1 × 10⁴

= 41000

So, the number  4.1 × 10⁴ in standard notation is 41000.

Problem 11 :

6.4 × 10²

Solution :

= 6.4 × 10²

= 640

Problem 12 :

6.91 × 10^-2

Solution :

= 6.91 × 10^-2

= 0.0691

Problem 13 :

An object with a lesser density than water will float. An object with a greater density than water will sink. Use each given density (in kilograms per cubic meter) to explain what happens when you place a brick and an apple in water.

Water: 1.0 × 10³       Brick: 1.84 × 10³       Apple: 6.41 × 10

Solution :

Water = 1.0 x 10³

Since we have positive exponent, moving the decimal three digits to the right, we get

= 1000 kg per cubic meter

Brick = 1.84 x 10³

Moving the decimal three digits to the right, we get

= 1840 kg per cubic meter

Apple = 6.41 x 10

= 64.1 kg per cubic meter.

The apple is less dense than water, so it will fl oat. The brick is denser than water, so it will sink.

Problem 14 :

A dog has 100 female fleas. How much blood do the fleas consume per day?

A female flea consumes about 1.4 x 10^-5 liter of blood per day.

Solution :

Quantity of blood cunsuming by female flea = 1.4 x 10^-5 liter

Required quantity of blood consumed by 100 female fleas,

= 1.4 x 10^-5 x 100

Multiplying 1.4 by 100 we get 140

= 140 x 10^-5

Since we have negative exponent and the power 5, we have to move the decimal 5 digits to the left. So, 0.00140 liters.

1 liter = 1000 ml

Conversion from liter to ml :

= 0.00140 x 1000

= 1.4 ml

Problem 15 :

Describe and correct the error in writing the number in standard form.

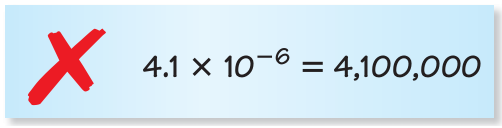
Solution :

Given that,

4.1 x 10^-6 

Since we have negative exponent, we have to move the decimal to the left of 6 digits.

0.0000041

The error is, instead of moving the decimal to the right, they moved to the left.

Problem 16 :

A googol is 1.0 × 10¹⁰⁰. How many zeros are in a googol?

Solution :

= 1.0 × 10¹⁰⁰

Since we have the power 100, we may have to move the decimal 100 digits to the right. We have only one 0, we may have to 100 digits, other than one 0 we may have to use 99 more zeroes.

Problem 17 :

The table shows the surface temperatures of five stars.

a. Which star has the highest surface temperature?

b. Which star has the lowest surface temperature?

Solution :

Surface temperature in Betelgeuse = 6.2 x 10³

Moving 3 digits to the right,

= 6200 F

Surface temperature in Bellatrix = 3.8 x 10⁴

Moving 4 digits to the right,

= 38000 F

Surface temperature in Sun = 1.1 x 10⁴

Moving 4 digits to the right,

= 11000 F

Surface temperature in Aldebaran = 7.2 x 10³

Moving 3 digits to the right,

= 7200 F

Surface temperature in Rigel = 2.2 x 10⁴

Moving 4 digits to the right,

= 22000 F

a.  Bellatrix (38000 F) has the highest surface temperature.

b. Betelgeuse (6200 F) has the lowest surface temperature.