CONGRUENT CHORDS AND CENTRAL ANGLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If two chords of a circle are congruent, then they determine central angles which are equal in measure.
Problem 1 :
Find the value of x.
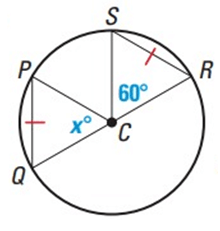
Solution :
PQ = SR
m∠SCR = 60˚
So, m∠SCR = m∠PCQ = 60˚
x = 60˚
Problem 2 :
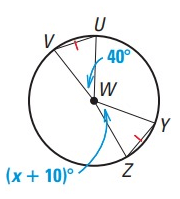
Solution :
The arc lengths are the same and the corresponding angles are the same.
UV = YZ
x + 10˚ = 40˚
x = 40˚ - 10˚
x = 30˚
Problem 3 :
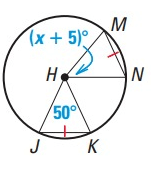
Solution :
The arc lengths are the same and the corresponding angles are the same.
MN = KJ
x + 5˚ = 50˚
x = 50˚ - 5˚
x = 45˚
Problem 4 :
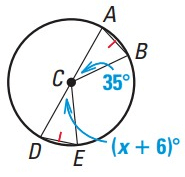
Solution :
The arc lengths are the same and the corresponding angles are the same.
AB = DE
x + 6˚ = 35˚
x = 35˚ - 6˚
x = 29˚
Problem 5 :
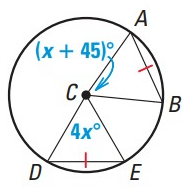
Solution :
The arc lengths are the same and the corresponding angles are the same.
AB = DE
x + 45˚ = 4x˚
4x - x = 45˚
3x = 45˚
x = 15˚
Problem 6 :
In the diagram below, AD and BE are diameters of ʘF. Find the measures.
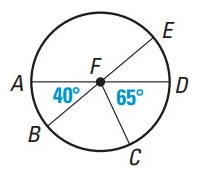
1) m arc
DE 2) m arc BC
3) m arc AE 4) m arc BCD
5)m arc ABC 6) m arc ADE
Solution :
40 + ∠BFC + 65 = 180
105 + ∠BFC = 180
∠BFC = 180 - 105
∠BFC = 75
∠BFC + ∠CFD + ∠DFE = 180
75 + 65 + ∠DFE = 180
140 + ∠DFE = 180
∠DFE = 180 - 140
∠DFE = 40
1) m arc DE = 40
2) m arc BC = 75
3) m arc AE :
∠AFB + ∠BFC + ∠CFD + ∠DFE = Measure of arc AE
40 + 75 + 65 + 40 = Measure of arc AE
Measure of arc AE = 220
4) m arc BCD :
∠BFC + ∠BCD = Measure of arc BCD
75 + 65 = Measure of arc BCD
Measure of BCD = 140
5) m arc ABC :
∠AFB + ∠BFC = Measure of arc ABC
40 + 75 = Measure of arc ABC
Measure of arc ABC = 115
6) m arc ADE :
∠DFE = 40 = m arc ADE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling