COMPOSITION OF FUNCTIONS FROM THE GRAPH
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Using the graphs below, evaluate f (g(1))
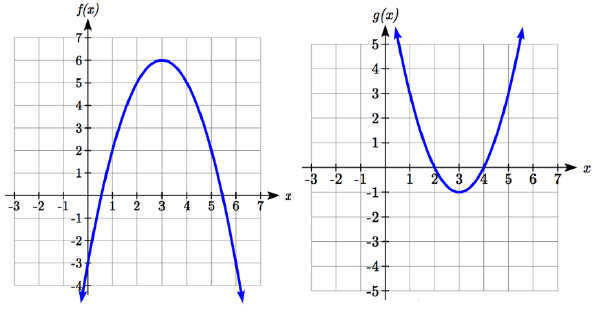
Solution :
f (g(1))
The value of g(1) from the graph of g(x) is 3.
So, f (g(1)) = f(3)
Value of f(3) from the graph f(x) is 6.
Then, the value of f (g(1)) is 6.
Example 2 :
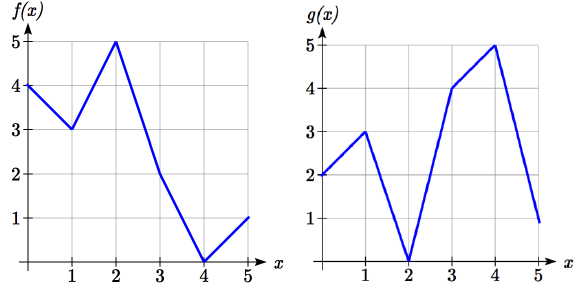
Use the graphs to evaluate the expressions below.
(i) f (g(3)) (ii) f (g (1)) (iii) g( f (1)) (iv) g ( f (0))
(v) f( f (5)) (vi) f ( f (4)) (vii) g(g(2)) (viii) g ( g (0))
Solution :
(i) f (g(3))
From the graph of g(x), first we find g(3).
g(3) = 4
f (g(3)) = f(4)
From the graph f(x), we find f(4).
The value of f(4) is 0. So, f(g(3)) = 0.
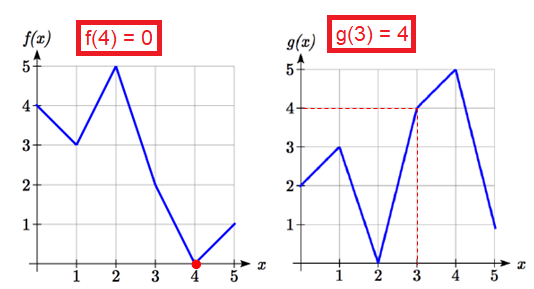
(ii) f (g (1))
Value of g(1) = 3, then f (g (1)) = f(3)
From the graph of f(x), the value of f(3) is 2.
(iii) g( f (1))
Value of f(1) = 3, then g (f (1)) = g(3)
From the graph of g(x), the value of g(3) is 4.
(iv) g ( f (0))
Value of f(0) = 4, then g (f (0)) = g(4)
From the graph of g(x), the value of g(4) is 5.
(v) f( f (5))
Value of f(5) = 1, then f (f (5)) = f(1)
From the graph of f(x), the value of f(1) is 3.
(vi) f ( f (4))
Value of f(4) = 0, then f (f (4)) = f(0)
From the graph of g(x), the value of f(0) is 4.
(vii) g(g(2))
Value of g(2) = 0, then g (g (2)) = g(0)
From the graph of g(x), the value of g(0) is 2.
(viii) g ( g (0))
Value of g(0) = 2, then g (g (0)) = g(2)
From the graph of g(x), the value of g(2) is 0.
Example 3 :
Use the graphs to evaluate the composition of functions.
(i) (g ∘ f)(1)
(ii) (g ∘ f)(5)
(iii) (f ∘ g)(0)
(iv) (f ∘ g)(2)

Solution :
(i) (g ∘ f)(1) = g[f(1)]
The value of f(1) is -1.
g[f(1)] = g(-1)
The value of g(-1) is 3.
(g ∘ f)(1) = 3
(ii) (g ∘ f)(5) = g[f(5)]
The value of f(5) is 1.
g[f(5)] = g[1]
The value of g(1) is 4.
(g ∘ f)(5) = 4
(iii) (f ∘ g)(0) = f[g(0)]
The value of g(0) is 5.
f[g(0)] = f(5)
The value of f(5) is 1.
(iv) (f ∘ g)(2) = f[g(2)]
The value of g(2) is 2.
f[g(2)] = f(2)
The value of f(2) is -2.
(f ∘ g)(2) = -2
Example 4 :
Use the graph to find each value.
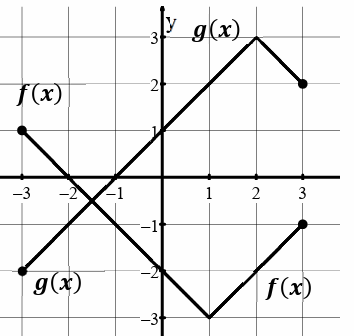
Find
a) f( g (2) )
b) (g ∘ f) (3)
c) g ( f (2) )
Solution :
a) f( g (2) ) = f[g(2)]
When input is 2, for the function g(x) the output is 3
= f [3]
When input is 3 for the function f(x), the output is -1
= -1
So, the value of f( g (2) ) is -1.
b) (g ∘ f) (3) = g [ f(3) ]
When input is 3, for the function f(x) the output is -1
= g [-1]
When the input is -1, the output for the function g(x) is 0.
= 0
c) g ( f (2) ) = g [ f(2) ]
When input is 2, the output for the function f(x) is -2
= g[-2]
When input is -2, the output for the function g(x) is 0.
= 0
Example 5 :
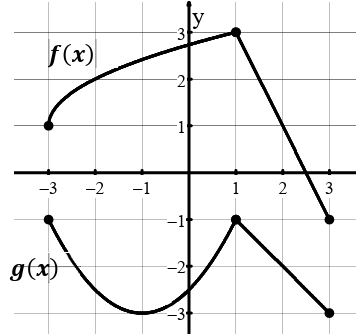
Find
a) f( g(2) )
b) (f ∘ g) (-1)
c) g ( f(1) )
Solution :
a)
f( g(2) ) = f[g(2)]
= f[-2]
= 2
b)
(f ∘ g) (-1) = f[g(-1)]
= f(-3)
= 1
c)
g ( f(1) ) = g[f(1)]
= g[3]
= -3
The first of the two graphs shows two functions 𝑓 𝑎𝑛𝑑 𝑔. The second shows two functions ℎ 𝑎𝑛𝑑 𝑘. Use the graphs to compute the following:
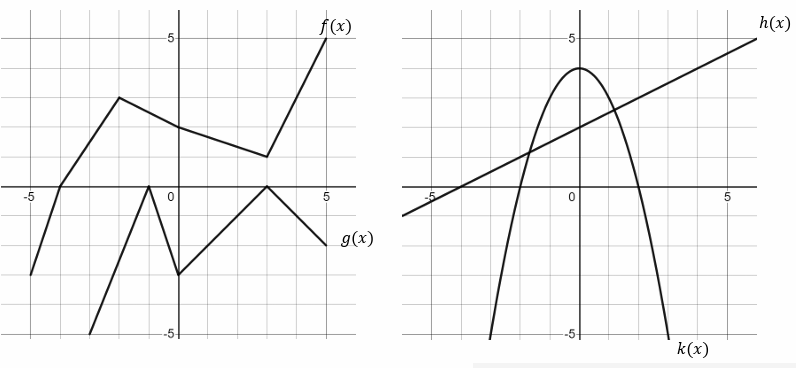
|
a) (𝑔 ◦ 𝑓) (−4) = b) (𝑓 ◦ 𝑔) (3) = c) (𝑓 ◦ 𝑓) (−2) = d) (𝑔 ◦ 𝑔) (3) = e) (𝑔 ◦ 𝑓) (−5) = f) (𝑔 ◦ 𝑓) (−3) = g) (ℎ ◦ 𝑘) (0) = |
h) (ℎ ◦ 𝑘) (−1) = i) (ℎ ◦ 𝑘) (2) j) (ℎ ◦ 𝑘) (−3) = k) (𝑘 ◦ ℎ) (0) = l) (𝑘 ◦ ℎ) (2) = m) (𝑘 ◦ ℎ) (−4) = n) (𝑘 ◦ ℎ) (−2) = |
a)
(𝑔 ◦ 𝑓) (−4) = g[f(-4)]
= g[0]
= -3
b)
(𝑓 ◦ 𝑔) (3) = f[g(3)]
= f [0]
= 2
c)
(𝑓 ◦ 𝑓) (−2) = f[f(-2)]
= f[3]
= 1
d)
(𝑔 ◦ 𝑔) (3) = g[g(-3)]
= g[-5]
= undefined
e)
(𝑔 ◦ 𝑓) (−5) = g[f(-5)]
= g[-3]
= -5
f)
(𝑔 ◦ 𝑓) (−3) = g[f(-3)]
= g[1.5]
= -1.5
g)
(ℎ ◦ 𝑘) (0) = h[k(0)]
= h[4]
= 4
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling