COMPOSITION OF FUNCTION FROM ARROW DIAGRAM

Problem 1 :

The arrow diagrams defines the functions

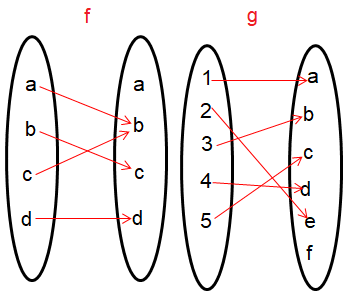
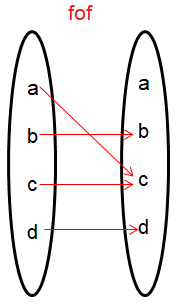
Find f∘f

i) f∘f :

Solution :

Input is a :

f∘f (a) = f [f(a)]

= f[b]

= c

So, (a, c)

Input is b :

f∘f (b) = f [f(b)]

= f[c]

= b

So, (b, b)

Input is c :

f∘f (c) = f [f(c)]

= f[b]

= c

So, (c, c)

Input is d :

f∘f (d) = f [f(d)]

= f[d]

= d

So, (d, d)

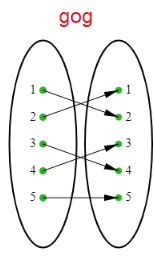
Problem 2 :

The arrow diagrams defines the functions

Find g∘g

i) g∘g :

Solution :

Input is 1 :

g∘g (1) = g [g(1)]

= g[4]

= 2

So, (1, 2)

Input is 2 :

g∘g (2) = g [g(2)]

= g[3]

= 1

So, (2, 1)

Input is 3 :

g∘g (3) = g [g(3)]

= g[1]

= 4

So, (3, 4)

Input is 4 :

g∘g (4) = g [g(4)]

= g[2]

= 3

So, (4, 3)

Input is 5 :

g∘g (5) = g [g(5)]

= g[5]

= 5

So, (5, 5).

The required relation is

g∘g is { (1, 2) (2, 1) (3, 4) (4, 3) (5, 5) }

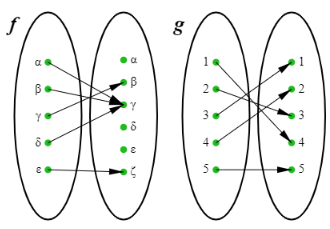
Problem 3 :

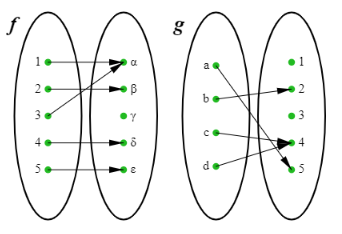
The arrow diagrams defines the functions

Find f∘g

i) f∘g :

Input is a :

f∘g (a) = f [g(a)]

= f[5]

= ε

So, (a,ε)

Input is b :

f∘g (b) = f [g(b)]

= f[2]

= β

So, (b, β)

Input is c :

f∘g (c) = f [g(c)]

= f[4]

= δ

So, (c, δ)

Input is d :

f∘g (d) = f [g(d)]

= f[4]

= δ

So, (d, δ)

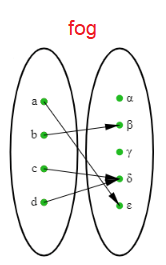
The required relation is,

{ (a,ε), (b, β), (c, δ), (d, δ) }

Problem 4 :

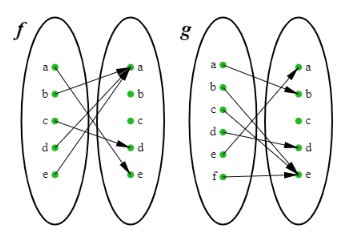
The arrow diagrams given define the functions

f : {a,b,c,d,e} → {a,b,c,d,e}

and

g : {a,b,c,d,e,f} → {a,b,c,d,e}.

Find the relation, f ∘ g

Solution :

Input is a :

f∘g (a) = f [g(a)]

= f[b]

= a

So, (a,a)

Input is b :

f∘g (b) = f [g(b)]

= f[e]

= a

So, (b, a)

Input is c :

f∘g (c) = f [g(c)]

= f[e]

= a

So, (c, a)

Input is d :

f∘g (d) = f [g(d)]

= f[d]

= a

So, (d, a)

Input is e :

f∘g (e) = f [g(e)]

= f[a]

= e

So, (e, e)

Input is f :

f∘g (f) = f [g(f)]

= f[e]

= a

So, (f, a)

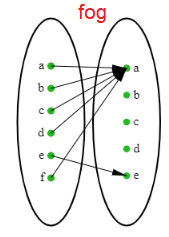
So, the required relation is

{ (a,a) (b, a) (c, a) (b, a) (d, a) (e, e) (f, a) }

Problem 5 :

The arrow diagrams given define the functions

f : {1, 2, 3, 4} → {α, β, γ, δ, ε, ζ}

and

g : {1, 2, 3, 4, 5, 6} → {1, 2, 3, 4, 5, 6}.

Find the function for g ∘ g

Solution :

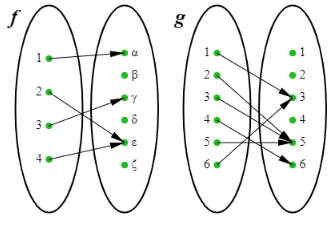
Solution :

Input is 1 :

g∘g (1) = g [g(1)]

= g[3]

= 5

So, (1, 5)

Input is 2 :

g∘g (2) = g [g(2)]

= g[5]

= 5

So, (2, 5)

Input is 3 :

g∘g (3) = g [g(3)]

= g[5]

= 5

So, (3, 5)

Input is 4 :

g∘g (4) = g [g(4)]

= g[6]

= 3

So, (4, 3)

Input is 5 :

g∘g (5) = g [g(5)]

= g[5]

= 5

So, (5, 5)

Input is 6 :

g∘g (6) = g [g(6)]

= g[3]

= 5

So, (6, 5)

So, the required relation is

{ (1, 5) (2, 5) (3, 5) (4, 3) (5, 5) (6, 5) }

COMPOSITION OF FUNCTION FROM ARROW DIAGRAM

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling