COMPLEX CONJUGATE ROOT THEOREM

Problem 1 :

Find all the zeroes of f(x) = x⁴ - 15x² + 38x - 60

Solution :

f(x) = x⁴ - 15x² + 38x - 60

Total number of roots for the given polynomial = 4

Signs of coefficients of f(x) = + -  + -

Number of sign changes = 3

So, 3 or 1 positive real roots.

f(-x) = (-x)⁴ - 15(-x)² + 38(-x) - 60

= x⁴ - 15x² - 38x - 60

Signs of coefficients of f(-x) = + -  - -

Number of sign changes = 1

Number of negative roots = 1

Using synthetic division, let us fix the solutions.

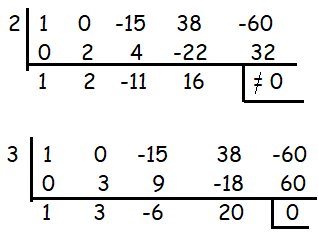
3 is one of the solutions,

the quotient = x³ + 3x² - 6x + 20

By solving the quotient, we will get the remaining zeroes.

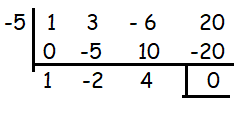
x² - 2x + 4 = 0

This quadratic equation is not solvable using factoring, using formula solving it.

a = 1, b = -2 and c = 4

Problem 2 :

A polynomial function with rational coefficients has the follow zeros. Find all additional zeros.

−5, i

Solution :

Since one root is in the form of a + ib, its conjugate will be the other root.

Then, the zeroes of the polynomial are -5, i and -i.

Problem 3 :

Write a quadratic equation whose root is 5 + i√2.

Solution :

Since one of the root is in the form of complex number, its conjugate will be the other root.

The roots are 5 + i√2 and 5 - i√2. Let a = 5 + i√2 and b = 5 - i√2

The required quadratic equation will be in the form,

x² - (a + b) x + ab = 0

a + b = 5 + i√2 + 5 - i√2 ==> 10

ab = (5 + i√2) (5 - i√2)

= 5² - (i√2)²

= 25 - (-1) (2)

= 27

x² - 10x + 27 = 0

So, the above quadratic equation will have two complex roots given in the question.

Problem 4 :

If 2 + i and 2 - i are the roots of the equation x² - 4x + c = 0, what is the value of c ?

Solution :

a = 2 + i and b = 2 - i

So, the required quadratic equation which has the above roots is 

x² - 4x + 5 = 0

Comparing the corresponding terms with  x² - 4x + c = 0

the value of c is 5.

Problem 5 :

If the solution set of x² + px + q = 0 is {1 +  i,1 - i}, find the value of p.

Solution :

a = 1 + i and b = 1 - i

So, the required quadratic equation which has the above roots is 

x² - 2x + 2 = 0

Comparing the corresponding terms with  x² + px + q = 0

the value of p is -20

Problem 6 :

If 2+3i is one root of a quadratic equation with real coefficients, what is the sum of the roots of the equation?

Solution :

Since the given root is in the form of complex number a + ib, its conjugate will be the other root.

a = 2 + 3i and b = 2 - 3i

Sum of the roots :

a + b = 2 + 3i + 2 - 3i

a + b = 4

So, the sum of roots is 4.

Problem 7 :

Write a polynomial function of least degree with integral coefficients that has the given zeros.

2i, −2i, 2 + 2i

Solution :

In the given roots, 2 + 2i does not have its conjugate. By considering its conjugate as other root, we will get 4 roots.

The required roots are 2i, -2i, 2 + 2i and 2 - 2i

Using the first two roots, we can get the quadratic equation. Using third and fourth roots, we can get the other quadratic equation. By multiplying these two quadratic equation, we can get a polynomial with the degree of 4

Quadratic equation with the roots 2i and  -2i :

Sum of roots = 0

Product of roots = 2i(-2i)

= 4i²

= +4

Quadratic equation which has the roots 2i and -2i is 

x² + 4 = 0

Quadratic equation with the roots 2+2i and  2-2i :

Sum of roots = 4

Product of roots = (2 + 2i)(2 - 2i)

= 4 - (2i)²

= 4 - 4(-1)

= 8

Quadratic equation which has the roots (2 + 2i) and (2 - 2i) is 

x² - 4x + 8 = 0

The required polynomial :

(x² + 4) (x² - 4x + 8) = 0

x⁴ - 4x³ + 8x² + 4x² - 16x + 32 = 0

x⁴ - 4x³ + 12x² - 16x + 32 = 0