COMPARING RATE OF CHANGE

A rate of change is a rate that describes how one quantity changes in relation to another quantity. If x is the independent variable and y is the dependent variable, then

Rate of change = Change in y/ Change in x

Rate of change from two points (x₁, y₁) and (x₂, y₂) :

Using the formula given below, we can find rate of change.

m = (y₂ - y₁)/(x₂ - x₁)

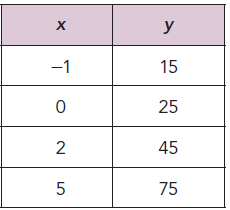
(x₁, y₁) ==> (-1, 15) and (x₁, y₁) ==> (0, 25)

m = (25 - 15) / (0 + 1)

m = 10/1

m = 10

Rate of change is positive.

Rate of change from graph :

To find slope or rate of change from the graph of the line, we can take two points on the line and horizontal change and vertical change.

Rate of change = Rise / Run

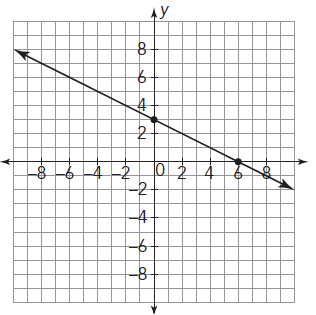
Take two points from the line and calculate horizontal and vertical changes.

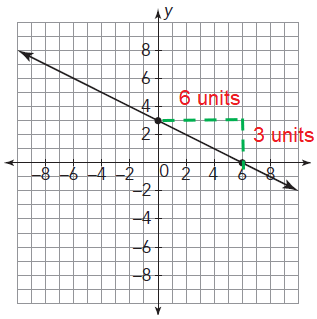
m = -3/6

m = -1/2

Examine each set of functions and determine which has the greater rate of change, if either. Explain your reasoning.

Problem 1 :

Solution :

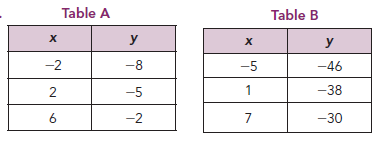
Rate of change from Table A :

Take any two points from table A. Say (-2, -8) and (2, -5).

(x₁, y₁) ==>  (-2, -8)  and (x₁, y₁) ==> (2, -5)

m = (y₂ - y₁)/(x₂ - x₁)

m  = (-5 + 8) / (2 + 2)

m  = 3/4

Rate of change from Table B :

Take any two points from table A. Say (-5, -46) and (1, -38).

(x₁, y₁) ==>  (-5, -46) and (x₁, y₁) ==> (1, -38)

m = (y₂ - y₁)/(x₂ - x₁)

m  = (-38+46) / (1+5)

m  = 8/6

m = 3/4

Both are having the same rate of change.

Problem 2 :

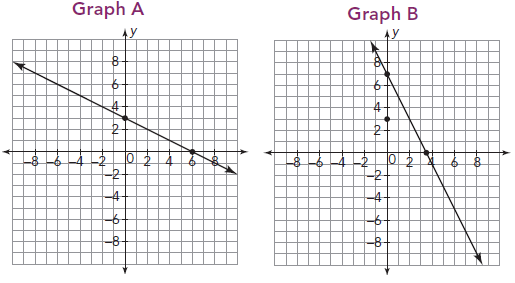
Solution :

Taking two points from Graph A :

(0, 3) and (6, 0)

Change in y = Rise = 0 - 3 ==> -3

Change in x = Run = 6 - 0 ==> 6

Slope = Rise / Run ==> -3/6 ==> -1/2

Taking two points from Graph B :

(0, 7) and (2, 3)

Change in y = Rise = 3 - 7 ==> -4

Change in x = Run = 2 - 0 ==> 2

Slope = Rise / Run ==> -4/2 ==> -2

Graph A is having greater rate of change.

Problem 3 :

Equation A  : 5x + 6y = 60

Equation B  : y = (-1/4)x  - 2

Solution :

From equation A :

To find rate of change from Equation A , we can convert the given equation into slope intercept form.

6y = -5x + 60

Divide by 6 on both sides.

y = (-5/6)x + (60/6)

y = (-5/6)x + 10

Rate of change = -5/6

From equation B :

y = (-1/4)x  - 2

Rate of change = -1/4

Rate of change in equation B is greater.

Problem 4 :

An ice cream shop is choosing a milk delivery service. The Spotted Cow charges $2.80 per gallon, plus a $2 delivery fee. Dairy Farms charges $2.10 per gallon, plus a $10 delivery fee.

Solution :

Let x be the charges per gallon and y be the total charge.

Creating the equation for the given situation, we get

Spotted cow charges :

y = 2.80x + 2

Rate of change = 2.80

Dairy Farms charges :

y = 2.10x + 10

Rate of change = 2.10

Spotted cow charge is greater.

Problem 5 :

The Metropolis Zoo recently celebrated the birth of two new baby pandas.

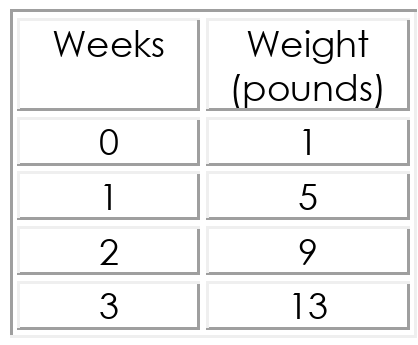
Mochi the panda cub has been measured and weighted each week since she was born.

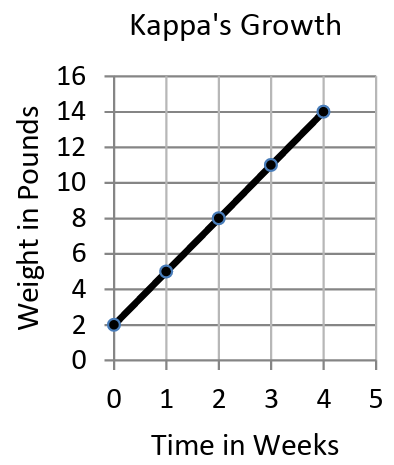
Mochi’s brother is Kappa. His weight has been charted on the graph below.

1. Which panda was heavier when born?

2. How fast is Mochi growing (rate of change)? How fast is Kappa growing (rate of change)?

3. Which panda will weigh more at 5 weeks?

Solution :

1)  y-intercept from the table = 1

Weight of Mochi = 1

y-intercept from the graph = 2

Weight of Kappa = 2

Kappa is heavier than Mochi.

2. Rate of change of Mochi :

(0, 1) and (1, 5)

Slope = (5 - 1) / (1 - 0)

= 4/1

= 4

Linear function for Mochi's growing rate : 

y = 4x + 1

Rate of change of Kappa :

(0, 2) and (1, 5)

Slope = (5 - 2) / (1 - 0)

= 3/1

= 3

Linear function for Kappa's growing rate : 

y = 3x + 2

3)