COMPARING DOT PLOTS VISUALLY

Problem 1 :

The dot plots show the heights of 15 high school basketball players and the heights of 15 high school softball players.

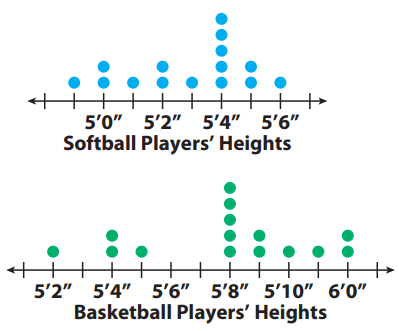
1)  Visually compare the shapes of the dot plots

2)   Visually compare the centers of the dot plots.

3)   Visually compare the spreads of the dot plots.

Solution :

1)

Softball players :

Heights of every softballs players is 5' 6''

Basketball players :

Most of basket ball players are 5' 8'' or higher.

Conclusion :

Softball player are shorter than basket ball players.

2)  

Softball: The data is centered around 5’4”.

Basketball: The data is centered around 5’8”.

This means that the most common height for the softball players is 5 feet 4 inches, and for the basketball players 5 feet 8 inches.

3)  

Softball: The spread is from 4’11” to 5’6”.

Basketball: The spread is from 5’2” to 6’0”.

There is a greater spread in heights for the basketball players

Problem 2 :

Visually compare the dot plot of heights of field hockey players to the dot plots for softball and basketball players.

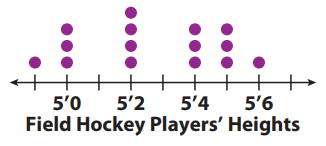
1) Spread

2) Shape

3) Center

Solution :

The spread of values in the dataset. We often use the range to measure this.

Largest value = 5' 6''

smallest value = 4' 11''

Range = 5' 6'' - 4' 11''

= 4' 18'' - 4' 11''

= 7''

2) The data is symmetric.

3)  The center point of the dataset. We often use the median to measure this.

Total number of data in the dot plot is 15 (odd).

Median = (15 + 1)/2

= 8^th value is the median

So, the median is 5' 2''

Problem 3 :

Numerically compare the dot plots of the number of hours a class of students exercises each week to the number of hours they play video games each week.

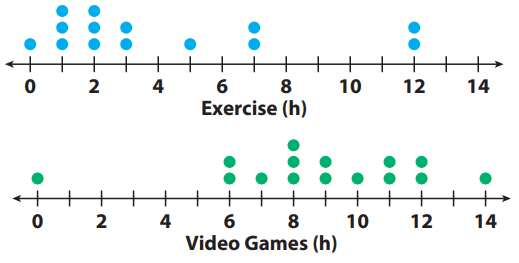
1)  Compare the shapes of the dot plots.

2)  Compare the centers of the dot plots by finding the medians.

3)  Compare the spreads of the dot plots by calculating the range.

Solution :

1)  Exercise: Most of the data is less than 4 hours.

Video games: Most of the data is 6 hours or greater.

2)  Median for exercise:2.5 hours.

Even though there are outliers at 12 hours, most of the data is close to the median.

Median for video games: 9 hours.

Even though there is an outlier at 0 hours, these values do not seem to affect the median.

3)  Exercise range with outlier: 12 - 0 = 12 hours

Exercise range without outlier: 7 - 0 = 7 hours

Video games range with outlier: 14 - 0 = 14 hours

Video games range without outlier: 14 - 6 = 8 hours

Problem 4 :

Calculate the median and range of the data in the dot plot.

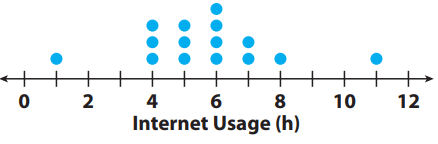
Solution :

Total number of values in the data set is = 15 (odd)

= (15 + 1)/2 th value

= 8th value

6 hours is the median of the data.

Range = Largest value - smallest value

= 11 - 1

= 10 hours

Problem 5 :

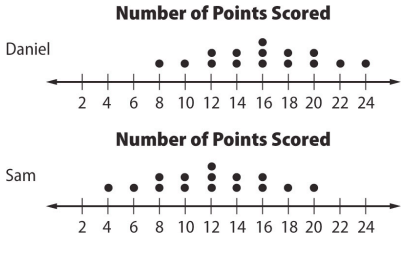
The double dot plot shows the number of points scored by Sam and Daniel in 15 basketball games. What is the difference between the medians?

Solution :

Total number of values of data set = 15

Daniel :

8th value is the median.

16 points is the median score of Daniel.

Sam :

16 points is the median score of Sam.

Problem 6 :

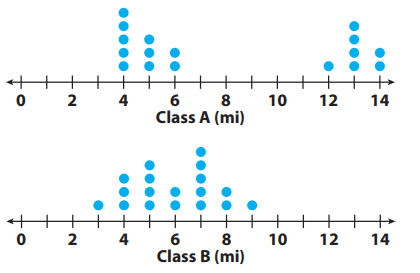
The dot plots show the number of miles run per week for two different classes. For 1–5, use the dot plots shown.

1. Compare the shapes of the dot plots.

2. Compare the centers of the dot plots.

3. Compare the spreads of the dot plots.

4. Calculate the medians of the dot plots.

5. Calculate the ranges of the dot plots

Solution :

1) Clustered around two areas in class A.

Clustered around only one area in class B.

2)  Calculating center :

Class A :

4, 4, 4, 4, 4, 5, 5, 5, 6, 6, 12, 13, 13, 13, 13, 14, 14

Total number = 17 (odd)

= (17+1)/2 ^th value

= 9^th value

6 is the center of class A.

Class B :

3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 7, 7, 7, 7, 7, 8, 8, 9

Total number = 18 (even)

= Average of 9^th value and 10^th value is mean

6 is the center of class A.

3)

The spread of class A is in between 4 to 14 miles.

The spread of class B is in between 3 to 9 miles.

4) Median for both classes is 6.

5)  Range of class A = 14 - 4 ==> 1 0

Range of class B = 9 - 3 ==> 6