COMPARING COEFFICIENTS OF POLYNOMIALS

Problem 1 :

2z – 3 is a factor of 2z³ – z² + az – 3. Find a and all zeros of the cubic.

Solution :

Since 2z – 3 is a factor, 2z - 3 = 0

2z = 3

z = 3/2

Given, 2z³ – z² + az – 3

z = 3/2 substitute the given equation.  

2(3/2)³ – (3/2)² + a(3/2) – 3 = 0

2(27/8) - 9/4 + 3a/2 - 3 = 0

27/4 - 9/4 + 3a/2 - 12/4 = 0

6/4 + 3a/2 = 0

3/2 + 3a/2 = 0

3/2 = -3a/2

a = -1

So, the value of a is -1.

 (2z³ – z² - z – 3) ÷ (2z - 3)

Using synthetic division.

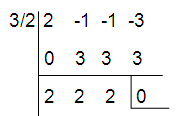
(2z² + 2z + 2) = 0

2(z² + z + 1) = 0

Dividing 2 on each sides.

z² + z + 1 = 0

a = 1, b = 1, c = 1

Using quadratic formula.

b² - 4ac = 1² - 4(1)(1)

= 1² - 4

= -3

z = -1 ± i3

Problem 2 :

3z + 2 is a factor of 3z³ – z² + [a + 1]z + a. Find a and all the zeros of the cubic.

Solution :

3z + 2 is a factor.

3z + 2 = 0

3z = -2

z = -2/3

Given, 3z³ – z² + [a + 1]z + a

3z³ – z² + az + z + a

z = -2/3 substitute the given equation.

So, the value of a is 6.

 (3z³ – z² + [a + 1]z + a) ÷ (3z + 2)

3z³ - z² + [6 + 1]z + 6 ÷ (3z + 2)

3z³ - z² + 7z + 6 ÷ (3z + 2)

Using synthetic division.

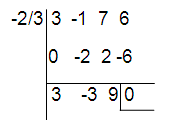
3z² - 3z + 9 = 0

3(z² - z + 3) = 0

Equating each factor to 0, we get

z = 0

z(z² - z + 3) = 0

a = 1, b = -1, c = 3

Using quadratic formula.

b² - 4ac = (-1)² - 4(1)(3)

= 1 - 12

= -11

Problem 3 :

Both 2x + 1 and x – 2 are factors of P(x) = 2x⁴ + ax³ + bx² – 12x – 8. Find a and b and all zeros of P(x).

Solution :

2x + 1 and x – 2 are factors

P(x) = 2x⁴ + ax³ + bx² – 12x – 8

x = -1/2 substitute the given equation.

P(-1/2) = 2(-1/2)⁴ + a(-1/2)³ + b(-1/2)² – 12(-1/2) – 8 = 0

2(1/16) + a(-1/8) + b(1/4) + 6 - 8 = 0

1/8 - (a/8) + (b/4) - 2 = 0

-(a/8) + (b/4) + (1/8) - 2 = 0

-(a/8) + (b/4) = 15/8

-a + 2b = 15 -----(1)

x = 2 substitute the given equation.

P(x) = 2x⁴ + ax³ + bx² – 12x – 8

2(2)⁴ + a(2)³ + b(2)² – 12(2) – 8 = 0

 32 + 8a + 4b - 24 - 8 = 0

8a + 4b = 0

Dividing by 4, we get

2a + b = 0 ----(2)

2 (1) + (2) ==> 

-2a + 4b + 2a + b  = 30 + 0

5b = 30

b = 6

Applying the value of b in (1), we get

-a + 2(6) = 15

-a + 12 = 15

-a = 15 - 12

-a = 3

a = -3

P(x) = 2x⁴ - 3x³ + 6x² – 12x – 8

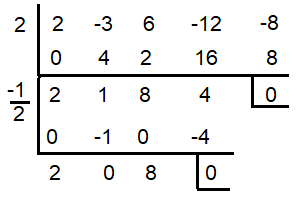
2x² + 8 = 0

Dividing the equation by 2, we get

x² + 4 = 0

x² = -4

x = ±i2

The zeroes are x = ±i2, x = -1/2 x = 2

Problem 4 :

x + 3 and 2x – 1 are factors of 2x⁴ + ax³ + bx² + ax + 3. Find a and b and hence determine all zeros of the quartic.

Solution :

x + 3 and 2x – 1 are factors.

2x⁴ + ax³ + bx² + ax + 3

x  = -3 substitute the given equation.

2(-3)⁴ + a(-3)³ + b(-3)² + a(-3) + 3 = 0

2(81) - 27a + 9b - 3a + 3 = 0 

162 - 30a + 9b + 3 = 0

165 - 30a + 9b = 0

-10a + 9b = -165

-10a + 3b = -55    ---(1)

x = 1/2 substitute the given equation.

5a + 2b = -25 ---(2)

(1) + 2(2)

-10a + 3b + 10a + 4b = -55 - 50

7b = 105

b = 15

Applying the value of n in (1), we get

5a + 30 = -25

5a = -55

a = -11

Problem 5 :

x³ + 3x²  - 9x + c has two identical linear factors. Prove that c is either 5 or -27 and factories the cubic into linear factors in each case.

Solution :

x³ + 3x²  - 9x + c

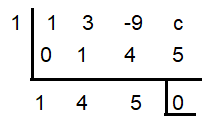
If x = 1 is a solution, then x -1 will be a factor, then the value of c will be -5.

Since we cannot factories x² + 4x + 5

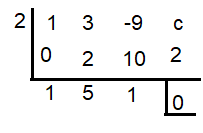
(x - 2) is a factor, then c will be -2.

(x³ + 3x²  - 9x + c) ÷ (x - 3)

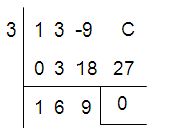
(x - 3) is a factor, then the value of C is -27.

P(x) = x² + 6x + 9

= (x + 3) and (x + 3)

= (x + 3)²

So, P(x) = (x  - 3) (x + 3)².

Problem 6 :

3x³ + 4x² – x + m has two identical linear factors. Find m and find the zeros of the polynomial in all possible cases.

Solution :

3x³ + 4x² – x + m

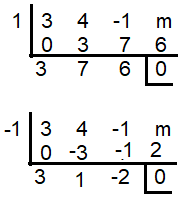
If (x - 1) is a factor, then the value of m will be -6. But the quadratic polynomial created by the left over will not have repeated factor.

If (x + 1) is a factor.

3x² + x - 2  = 0

(3x - 2) and  (x + 1) = 0

So, the repeated factor is (x + 1).