COLLINEAR POINTS AND CONGRUENT POINTS

Problem 1 :

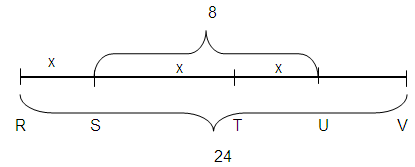
Given : RV = 24

SU = 8

RS = ST = TU

RS = ?

Solution :

Let RS = x

From the condition.

SU = ST + TU

8 = x + x

8 = 2x

8/2 = x

4 = x

So, the value of RS is 4.

Problem 2 :

Given : RV = 24

SU = 8

RS = ST = TU

UV = ?

Solution :

From the condition.

SU = ST + TU

8 = x  + x

8 = 2x

8/2 = x

4 = x

To find UV :

From the condition.

RV = RS + ST + TU + UV

24 = x  + x + x + UV

24 = 3x + UV

24 = 3(4) + UV

24 = 12 + UV

24 - 12 = UV

UV = 12

Problem 3 :

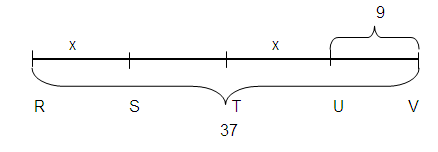
Given : RV = 37

RS = TU

UV = 9

ST + UV = 15

ST = ?

RS = ?

SU = ?

Solution :

ST + UV = 15

ST + 9 = 15

ST = 15 - 9

ST = 6

 RV = 37

Given condition  : RS = TU

Let RS = x

RV = RS + ST + TU + UV

37 = x + 6 + x + 9

37 = 2x + 15

37 - 15 = 2x

22 = 2x

x = 22/2

x = 11

RS = 11

SU = ST + TU

SU = 6 + 11

SU = 17

So, the value of ST = 6, RS = 11, SU = 17.

Problem 4 :

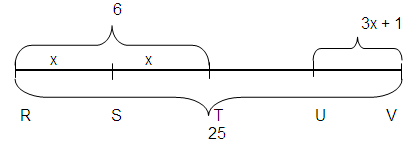
Given : RV = 25

RT = 6

RS = ST = TU

UV = 3x + 1

x = ?

Solution :

From the condition.

RV = RT + UV

25 = 6 + 3x + 1

25 =  7 + 3x

25 - 7 = 3x

18 = 3x

18/3 = x

6 = x

So, the value of x is 6.

Problem 5 :

Points F, X, and D are collinear, with F between X and D. Draw a diagram and solve for X, if FX = 2x + 13, FD = 7x - 6, and XD = 2x + 70.

Solution :

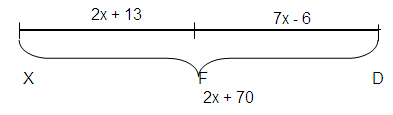
Given, FX = 2x + 13, FD = 7x - 6, and XD = 2x + 70

XD = XF + FD

2x + 70 = 2x + 13 + 7x - 6

2x + 70 = 9x + 7

70 - 7 = 9x - 2x

63 = 7x

63/7 = x

x = 9

So, the value of x is 9.

Problem 6 :

P, A, and Z are collinear. Z is between P and A. Draw a diagram and solve for x, given : ZP = 6x - 13, ZA = 9x + 27, and AP = 3x + 74.

Solution :

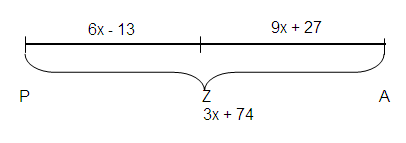
Given ZP = 6x - 13, ZA = 9x + 27, and AP = 3x + 74

AP = ZP + ZA

3x + 74 = 6x - 13 + 9x + 27

3x + 74 = 15x + 14

74 - 14 = 15x - 3x

60 = 12x

x = 60/12

x = 5

So, the value of x is 5.