CLASSIFYING POLYNOMIALS BY DEGREE AND NUMBER OF TERMS

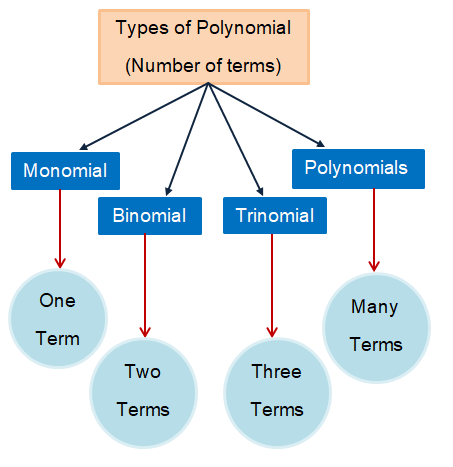
Classifying polynomials based on number of terms.

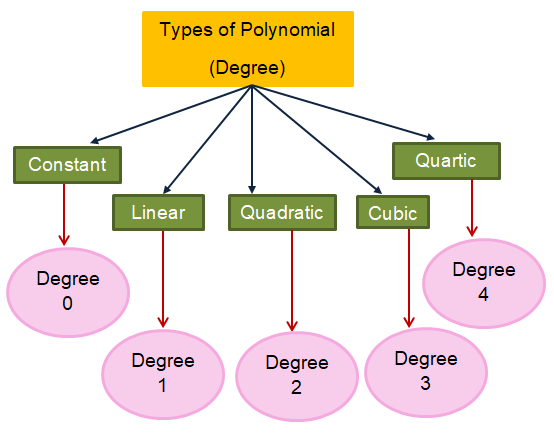
Classifying polynomials based on degree.

Give the name for the following polynomials based on power and degree of the polynomials.

Problem 1 :

3

Solution :

Degree of the polynomial = 0, number of terms = 1

Name of the polynomial :

Based on degree = Constant 

Based on number of terms = Monomial

Problem 2 :

-p² + 2

Solution :

Degree of the polynomial = 2, number of terms = 2

Name of the polynomial :

Based on degree = Quadratic 

Based on number of terms = Binomial

Problem 3 :

6x⁴ - 2x³

Solution :

Degree of the polynomial = 4, number of terms = 2

Name of the polynomial :

Based on degree = Quartic 

Based on number of terms = Binomial

Problem 4 :

 5n⁴ - n² - 2

Solution :

Degree of the polynomial = 4, number of terms = 3

Name of the polynomial :

Based on degree = Quartic 

Based on number of terms = trinomial

Problem 5 :

-2p⁴ + 10p⁶ + 5p²

Solution :

Degree of the polynomial = 6, number of terms = 3

Name of the polynomial :

Based on degree = polynomial

Based on number of terms = trinomial

Problem 6 :

9m + 5m² + 10m³ - 5

Solution :

Degree of the polynomial = 3, number of terms = 3

Name of the polynomial :

Based on degree = cubic

Based on number of terms = polynomial

Problem 7 :

8n² - n³ + 7n

Solution :

Degree of the polynomial = 3, number of terms = 3

Name of the polynomial :

Based on degree = cubic

Based on number of terms = trinomial