CLASSIFYING POLYGONS CONCAVE OR CONVEX

Convex polygon :

A convex polygon is a polygon with all interior angles less than 180^º and vertices are pointed outwards.

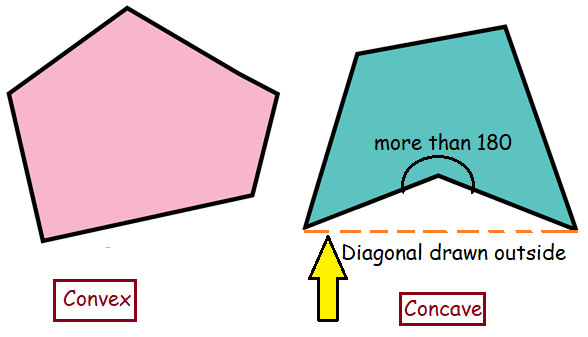
Concave polygon :

A concave polygon is a polygon that has at least one interior angle greater than 180 degrees. It must have at least four sides.

Problem 1 :

Match the type of polygon with the description.

Solution :

1. Convex polygon :

A convex polygon is a polygon with all interior angles less than 180^º and vertices are pointed outwards.

According to the given option for question (1) is E.

No line containing a side of the polygon passes through the interior of the polygon.

2. Concave polygon :

A concave polygon is a polygon that has at least one interior angle greater than 180 degrees. It must have at least four sides. 

According to the given option for question (2) is C.

Polygon that is not convex.

3. Equilateral polygon :

An equilateral polygon means all the sides are congruent..

According to the given option for question (3) is B.

All sides are congruent.

4. Equiangular polygon :

An equiangular polygon means all angles are congruent..

According to the given option for question (4) is D.

All interior angles are congruent.

5. Regular polygon :

Regular polygon is a polygon that is direct equiangular and equilateral.

According to the given option for question (5) is A.

Polygon that is both equilateral and equiangular.

Decide whether the polygon is convex or concave.

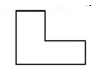
Problem 2 :

Solution :

By observing the figure,

This polygon is concave. Because, if one or more than one interior angles of the polygon is greater than 180^º.

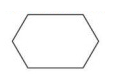
Problem 3 :

Solution :

By observing the figure,

This polygon is convex.  Because, a polygon is said to be convex if all the interior angles of the polygon are less than 180^º. 

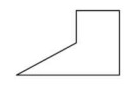
Problem 4 :

Solution :

By observing the figure,

This polygon is concave. Because, if one or more than one interior angles of the polygon is greater than 180^º.

Decide whether the polygon is equilateral, equiangular, or neither.

Problem 5 :

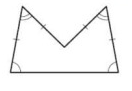
Solution :

By observing the figure,

It is neither polygon. Because sides are equal but angles are not equal.

Problem 6 :

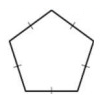
Solution :

By observing the figure,

A polygon is equilateral if all of its sides are congruent.

Problem 7 :

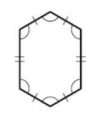
Solution :

By observing the figure,

A polygon is equiangular if all of its interior angles are congruent.

Decide whether the polygon is regular. Explain your answer.

Problem 8 :

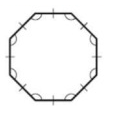
Solution :

By observing the figure, It is a regular polygon.

Regular polygon means all sides and all angles are congruent. So, regular polygon is equilateral and equiangular.

Problem 9 :

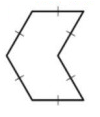
Solution :

By observing the figure, a polygon is equilateral if all of its sides are congruent.

Problem 10 :

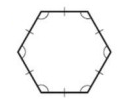
Solution :

By observing the figure, It is a regular polygon.

Regular polygon means all sides and all angles are congruent.