CLASSIFYING LOCATION AND TYPES OF DISCONTINUITY OF A FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
What is continuous ?
Functions that can be drawn without lifting up your pencil are called continuous functions. You will define continuous in a more mathematically rigorous way after you study limits.
Types of discontinuity :
There are three types of discontinuities:
i) Removable
ii) Jump and
iii) Infinite
Removable Discontinuity:
Removable discontinuities occur when a rational function has a factor with an x that exists in both the numerator and the denominator. Removable discontinuities are shown in a graph by a hollow circle that is also known as a hole. Below is the graph for
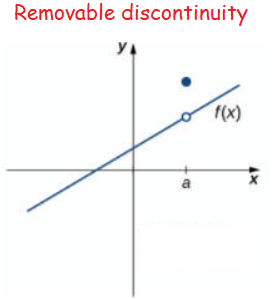
Jump discontinuity :
The function's curve would be labeled as discontinuous as it jumps from one point to another at the function's discontinuity point.
To better understand what is happening, we can split our function into two different sections, each approaching the jump from either direction. As either side of the function approaches the discontinuity, they are approaching their limit. The feature of approaching a limit on one side is known as a one-sided limit, however our function has two one-sided limits, and they have different values.
In short, the function approaches different values depending on which direction X is moving.
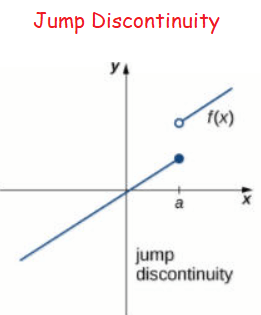
Infinite discontinuity :
An infinite discontinuity occurs when a function has a vertical asymptote on one or both sides. This is shown in the graph of the function below at x=1:
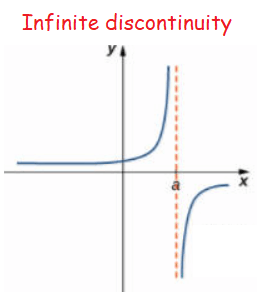
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Classify the locations and types of discontinuities of the following functions. Write the corresponding limits.
Problem 1 :
Solution :
When x - 1 = 0
x = 1
At x = 1, the given function f(x) will approach - infinity.
lim x->1 f(x) = -∞
Discontinuity of the function :
Yes, it is discontinuous at x = 1.
Types of discontinuity :
Infinite discontinuity.
Problem 2 :
Solution :
Here the common factor is (3 - √x), that can be removed.
Discontinuity of the function :
Yes, it is discontinuous at x = 9.
Types of discontinuity :
Removable discontinuity.
Evaluating limit :
Problem 3 :
Solution :
Discontinuity of the function :
Yes, it is discontinuous at x = -3.
Types of discontinuity :
Removable discontinuity.
Evaluating limit :
Problem 4 :
Solution :
Discontinuity of the function :
Yes, it is discontinuous at x = 0.
Types of discontinuity :
Jump discontinuity. Because the starting points of these curves are not same.
Evaluating limit :
Problem 5 :
The graph of
has
a) a vertical asymptote at x = 3
b) a horizontal asymptote at y = 1/3
c) a removable discontinuity at x = 3
d) an infinite discontinuity at x = 3
e) none of these
Solution :
It has removable discontinuity at x = 3
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling