CLASSIFY TRIANGLES BASED ON SIDES AND ANGLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The closed shape which is being covered by three sides is known as triangle.
Classification based on sides :
Based on the length of sides, we can classify triangles, those are
Based on Sides
|
Equilateral triangle : If all three sides are having equal lengths, then it is equilateral triangle. |
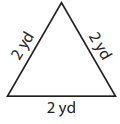 |
|
Scalene triangle : If all sides are having different measures, then it is scalene triangle. |
 |
|
Isosceles triangle : If only two sides of the triangle is equal, then it is isosceles triangle. |
 |
Based on Angles
|
Acute triangle : If all interior angles of the triangle, then it is acute triangle. |
 |
|
Obtuse triangle : If one the angle of triangle is obtuse, then it is obtuse triangle. |
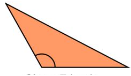 |
|
Right triangle : If one the angle of triangle is right angle, then it is right triangle. |
 |
Classify each triangle as equilateral,
isosceles, or scalene.
Problem 1 :
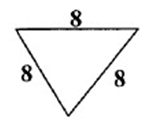
Solution :
The lengths of all the three sides are equal. So, the given triangle is an equilateral triangle.
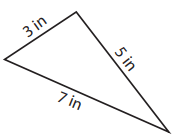
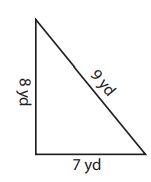
Problem 2 :
Solution :
The lengths of all the three sides are different. So, the given triangle is a scalene triangle.
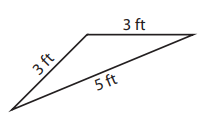
Problem 3 :
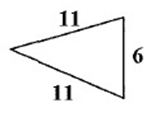
Solution :
The lengths of two of the sides are equal. So, the given triangle is an isosceles triangle.
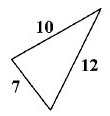
Problem 4 :
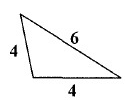
Solution :
The lengths of two of the sides are equal. So, the given triangle is an isosceles triangle.
Classify each triangle as acute, obtuse, right, or equiangular.
Problem 5 :
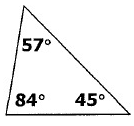
Solution :
i) All the given three angles are different .
ii) All the three angles are less than 90˚.
So, the given triangle is a acute triangle.
Problem 6 :
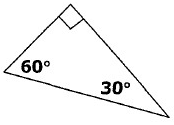
Solution :
i) All the given three angles are different.
ii) One of the angles is 90˚.
So, the given triangle is a right triangle.
Problem 7 :
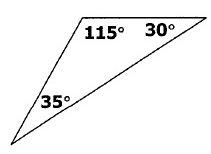
Solution :
i) All the given three angles are different.
i) One of the angles is greater than 90˚.
So, the given triangle is a obtuse triangle.
Problem 8 :
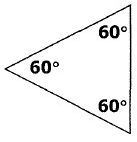
Solution :
i) All the given three angles are equal.
ii) All the three angles are less than 90˚.
So, the given triangle is a equilateral and acute triangle.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling