CHECK IF THE GIVEN IS ZERO OF POLYNOMIAL THEN SOLVE

To check if the given value is one of the zeroes of the polynomial, we have different ways.

i) Using remainder theorem

ii) Using long division

iii) Using synthetic division.

Remainder theorem :

Let us consider the given polynomial as p(x). If (x - a) is factor of the polynomial given, then p(a) will be zero. That is remainder will become zero when we divide a polynomial by its factor.

Using long division :

Converting the given value as factor and dividing the polynomial by this factor, we will get quotient and remainder. If the remainder is 0, then it is factor otherwise it is not.

By equating the quotient to 0, we will get other zeroes.

Using synthetic division :

If the given is a linear factor, equate that to 0 to find value of x. By equating the quotient to 0, we will get other zeroes. If the remainder is 0, then it is factor otherwise it is not.

For each of the following cubic equations one root is given. Determine the other roots of each cubic.

Problem 1 :

x3 + 3x2 – 6x – 8 = 0 has a root at x = 2.

Solution :

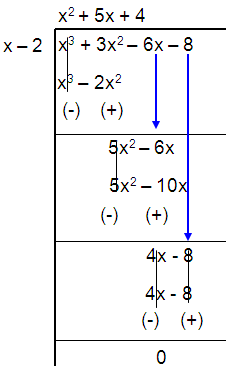
(x2 + 5x + 4) (x – 2) = 0

By using factorization

(x2 + 4x + x + 4) (x – 2) = 0

(x(x + 4) + 1(x + 4)) (x – 2) = 0

(x + 1) (x + 4) (x – 2) = 0

x = -1, x = -4, x = 2

So, the other root are x = -1, -4 and 2.

Problem 2 :

x3 + 2x2 – 21x + 18 = 0 has a root at x = 3.

Solution :

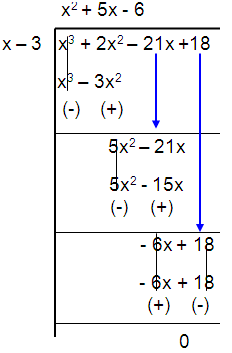
(x2 + 5x - 6) (x – 3) = 0

By using factorization

(x2 - 1x + 6x - 6) (x – 3) = 0

x(x - 1) + 6(x - 1) (x – 3) = 0

(x + 6) (x - 1) (x – 3) = 0

x = -6, x = 1, x = 3

So, the other roots are x = -6, x = 1 and x = 3.

Problem 3 :

x3 + 4x2 + 7x + 6 = 0 has a root at x = -2.

Solution :

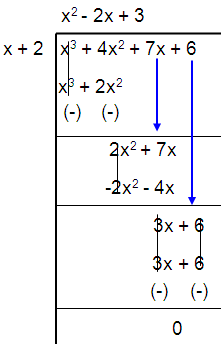
(x2 - 2x + 3) (x + 2) = 0

By using factorization

(x2 + 1x - 3x + 3) (x + 2) = 0

x(x + 1) - 3(x + 1) (x + 2) = 0

(x - 3) (x + 1) (x + 2) = 0

x = 3, x = -1, x = -2

So, the other root is x = 3, x = -1 and x = -2.

Problem 4 :

2x3 + 9x2 + 3x – 4 = 0 has a root at x = -4.

Solution :

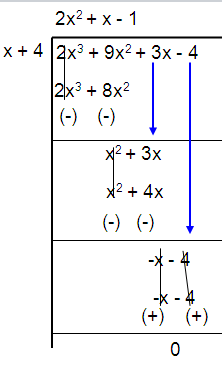
(2x2 + x - 1) (x + 4) = 0

By using factorization

(2x2 - 1x + 2x - 1) (x + 4) = 0

x(2x - 1) + 1(2x - 1) (x + 4) = 0

(x + 1) (2x - 1) (x + 4) = 0

x = -1, 2x = 1, x = -4

x = -1 x = 1/2, x = 4

So, the other root is x = 1/2, x = -1 and x = -4.

For each of the following cubic equations use synthetic division to determine if the given value of x is a root of the equation. Where it is, determine the other roots of the equation.

Problem 5 :

Is x = -2 a root of the equation x3 + 9x2 + 26x + 24 = 0 ?

Solution :

x3 + 9x2 + 26x + 24 = 0

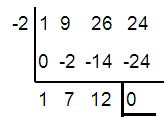
x2 + 7x + 12= 0

x2 + 4x + 3x + 12 = 0

x(x + 4) + 3(x + 4) = 0

(x + 3) (x + 4)= 0

x  = -3 x = -4

Hence, other roots are x = -3, x = -4 and x = -2.

Problem 6 :

Is x = 4 a root of the equation x3 - 6x2 + 9x + 1 = 0 ?

Solution :

x3 - 6x2 + 9x + 1 = 0

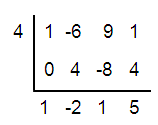
Hence, x = 4 is not a root.

Problem 7 :

Is x = -1 a root of the equation x3 + 6x2 + 3x - 5 = 0 ?

Solution :

x3 + 6x2 + 3x - 5 = 0

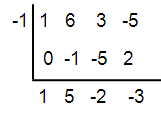
Hence, x = -1 is not a root.

Problem 8 :

Is x = 2 a root of the equation x3 + 2x2 - 20x + 24 = 0 ?

Solution :

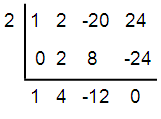
x2 + 4x – 12 = 0

x2 + 6x - 2x - 12 = 0

x(x + 6) - 2(x + 6) = 0

(x - 2) (x + 6)= 0

x = 2 x = -6

Hence, other roots are x = 2, x = -6 and x = 2.

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More