CHECK IF THE GIVEN NUMBER IS PERFECT SQUARE

Check if the Given Number is Perfect Square Using Long Division method :

Problem 1 :

Check if 53824 is a perfect square ?

Solution :

Using long division, let us check if the number is perfect square. Starting from the last digit, put comma for every two digits. 

That is, 5, 38, 24

Decompose 5 as product of two same values.

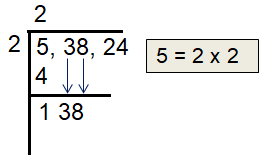
Multiply the quotient 2 by 2, we get 4.

Put the same digit near 4 and near 2 at the quotient.

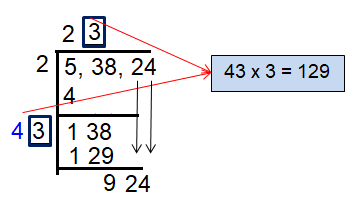
Now multiply the new quotient by 2 to get the next step.

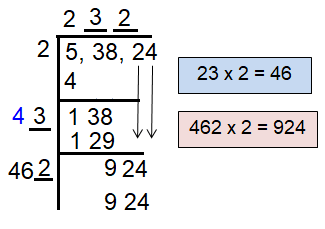
Since the remainder is 0, we say 53824 is a perfect square.

Problem 2 :

Check if 294 is a perfect square, if it is not find the least number must be multiplied to make it a perfect square.

(a)   2    (b)  3   (c)  6     (d)  24

Solution :

Decomposing 294, we get

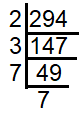
The given number 294 is not a perfect square.

From the prime factorization, it is clear in 7 we have two sevens. But we have only one 2 and 3. In order to make it as perfect square, we need one more 2 and one more 3.

294 = 2 x 3 x 7 x 7

To make it as perfect square,

294 = 2 x 3 x 7 x 7 x 2 x 3

So, the required number is 6.

Problem 3 :

The least perfect square number divisible by 3, 4, 5, 6 and 8 is

(a)  900  (b) 1200   (c) 2500   (d)  3600

Solution :

Since the required number is divisible by 3, 4, 5, 6 and 8, it should be the multiple of all.

To find the least number which is divisible by all above, we find the least common multiple of all.

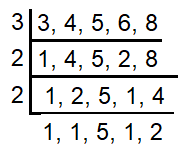
LCM (3, 4, 5, 6, 8) = 120

The required number should be a multiple of 120

(a) 900 is not a multiple of 120 even though it is perfect square.

(b) 1200 is not a perfect square.

(c)  2500 is a perfect square but not a multiple of 120.

(d) 3600 is a perfect square as well multiple of 120.

So, option d is correct.

Problem 4 :

The least perfect square, which is divisible by each of 21, 36 and 66 is 

(a)  213444   (b)  214344   (c) 214434  (d)  231444

Solution :

21 = 3 x 7

36 = 3² x 2²

66 =  2 x 3 x 11

LCM (21, 36, 66) = 3² x 2² x 7 x 11

= 2772

To make this least common multiple as perfect square, we need one 7 and one 11.

2772 = 3² x 2² x 7 x 11 x (7 x 11)

2772 x 77 ==> 213444

So, option a is correct.