CHECK IF THE GIVEN FIGURES ARE SIMILAR

Are the two figures similar ? If so, state the scale factor.

Problem 1 :

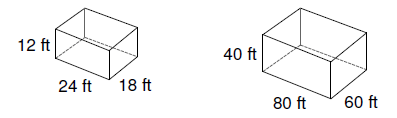
Solution :

Comparing the corresponding sides, we get

Since the ratios are equal, the given shapes are similar. The scale factor is 3 :10.

Problem 2 :

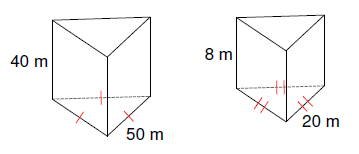
Solution :

Comparing the corresponding sides,

40/8 = 5

50/20 ≠ 5

Since the ratios are not same, the shapes are not similar.

Problem 3 :

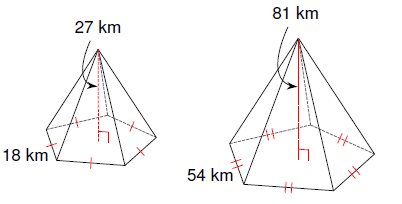
Solution :

Since the ratios are same, the shapes are similar. The required scale factor is 1 : 3.

Problem 4 :

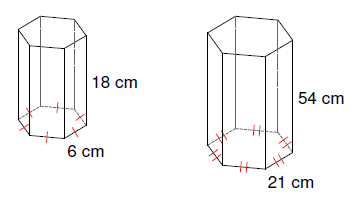
Solution :

Comparing the corresponding sides,

18/54 = 1/3

6/21 = 2/7

Since the ratios are not same, they are not similar shapes.

Each pair of figures is similar. Use the information given to find the scale factor of the figure on the left to the figure on the right. 

Problem 5 :

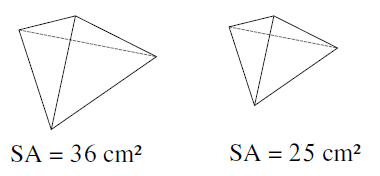
Solution :

Surface area of large shape : Surface area of small shape

= 36 : 25

k² = 36/25

k = √36/25

k = 6/5

So, the scale factor is 6 : 5.

Problem 6 :

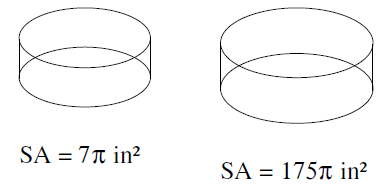
Solution :

Surface area of small shape : Surface area of large shape

= 7π : 175π

k² = 7π/175π

k² = 1/25

k = √1/25

k = 1/5

So, the scale factor is 1 : 5.

Problem 7 :

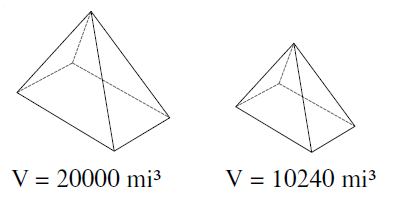
Solution :

Volume of small shape : Volume of large shape

10240 : 20000

k³ = 10240/20000

k³ = 64/125

k = ∛(64/125)

k = 4/5

So, the scale factor is 4 : 5.

Problem 8 :

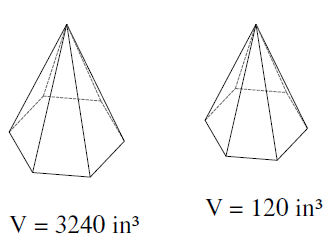
Solution :

Volume of large shape : Volume of small shape

= 3240 : 120

k³ = 3240/120

k³ = 27

k = ∛27

k = 3

So, the scale factor is 3 : 1.