CHECK IF THE FUNCTION IS CONTINUOS AND DIFFERENTIABLE FROM GRAPH

Check If the Function is Continuous from the Graph

What is continuity ?

A function is continuous if its graph is an unbroken curve; that is, the graph has no holes, gaps, or breaks.

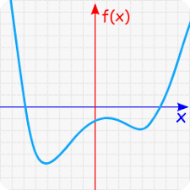
There are three types of discontinuity :

1) Infinite discontinuity

2) Jump discontinuity

3) Removable discontinuity

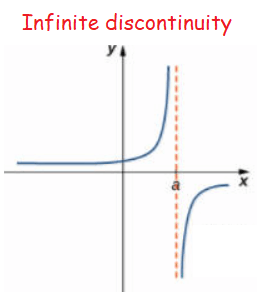
Non removable or infinite discontinuity :

An infinite discontinuity occurs when a function has a vertical asymptote on one or both sides. This is shown in the graph of the function below at x = a.

lim x->a- f(x) = ∞

lim x->a+ f(x) = -∞

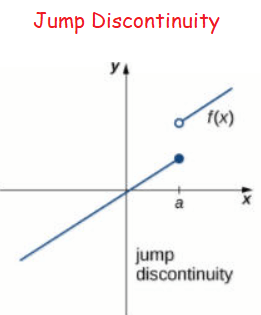
Jump discontinuity :

The function's curve would be labeled as discontinuous as it jumps from one point to another at the function's discontinuity point.

In short, the function approaches different values depending on which direction X is moving.

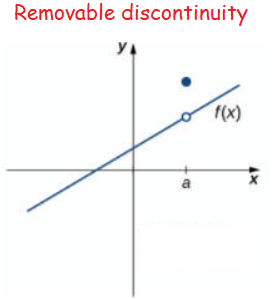
Removable Discontinuity:

Removable discontinuities occur when a rational function has a factor with an x that exists in both the numerator and the denominator. Removable discontinuities are shown in a graph by a hollow circle that is also known as a hole. Below is the graph for

For the following figure, check whether the function is continuous, differentiable, both or neither at x = c.

Problem 1 :

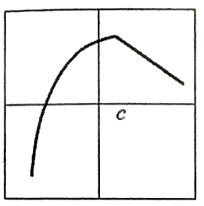
Solution :

Continuous or not :

The function is continuous.

Differentiable or not :

The function is not differentiable at x = c, because we can draw a vertical tangent line.

Problem 2 :

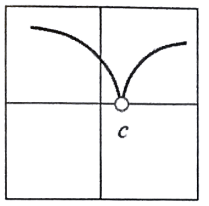
Solution :

Continuous or not :

The function is not continuous.

Differentiable or not :

Since it has discontinuity it is not differentiable.

So, answer is neither.

Problem 3 :

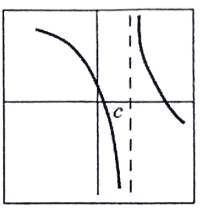
Solution :

Continuous or not :

The function is not continuous. It has infinite discontinuity.

Differentiable or not :

Since it has discontinuity it is not differentiable. 

So, answer is neither.

Problem 4 :

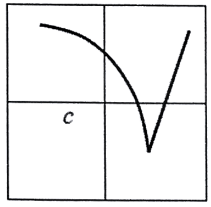
Solution :

Continuous or not :

The function is continuous.

Differentiable or not :

It is differentiable at x = c, but at the sharp point it is not differentiable.

Problem 5 :

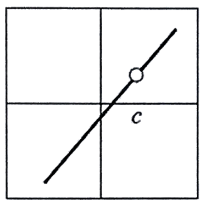
Solution :

Continuous or not :

The function is discontinuous, it has removable discontinuity at x = c.

Differentiable or not :

Since it has discontinuity at x = c, it is not differentiable.

So, the answer is both.

Problem 6 :

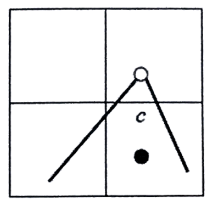
Solution :

Continuous or not :

The function is discontinuous, it is removable discontinuity at x = c.

Differentiable or not :

Since it has discontinuity at x = c, it is not differentiable.

So, the answer is both.

Problem 7 :

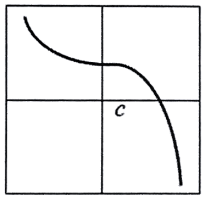
Solution :

Continuous or not :

The function is continuous.

Differentiable or not :

It is continuous, have same slope by approaching limi x->c from both sides, they are equal, we cannot draw the vertical tangent line. So, it is differentiable.

So, the answer is both.

Problem 8 :

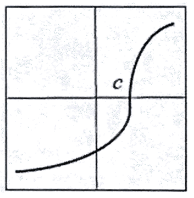
Solution :

Continuous or not :

The function is continuous.

Differentiable or not :

At x = c, we can draw the vertical tangent line. So, it is not differentiable.