CHARACTERISTICS OF EXPONENTIAL FUNCTIONS

An exponential function is non linear function of the form

y = ab^x, where a ≠ 0 and b ≠ 1 and b > 0

Where a > 0 and b > 1, then the function is an exponential growth function.
Where a > 0 and 0 < b < 1, then the function is an exponential decay function.

Horizontal asymptote :

Horizontal asymptotes are horizontal lines that the graph of the function approaches as x tends to +∞ or −∞.

For the function in the form

y = ab^x

horizontal asymptote is y = 0

For the function in the form

y = ab^x-h + k

horizontal asymptote is y = k

Domain :

For exponential function, domain is all set of real values.

Range :

Set of possible outputs is range. If there is no reflection

y = (0, ∞)

If it reflection across y-axis, then domain will be

y = (k, -∞)

Find the following characteristics of the exponential functions given below.

1) Graph the function

2) a = ?

3) b = ?

4) y - intercept

5) x - intercept

6) Domain

7) Range

8) Asymptote

9) Increasing interval

10) Decreasing interval

Problem 1 :

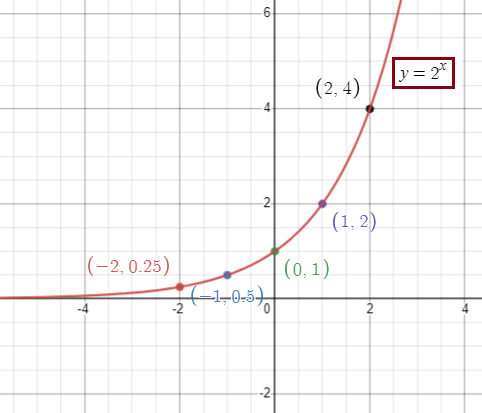
y = 2^x

Solution :

a = 1, b = 2 > 0 (exponential growth)

Horizontal asymptote is y = 0.

Put x = 0, y = 2⁰

So, y-intercept is (0, 1).

1) Graph the function

2) a = 1

3) b = 2

4) y - intercept = 1

5) x - intercept = none

6) Domain = (-∞, ∞)

7) Range = (0, ∞)

8) Asymptote, y = 0

9) Increasing interval

(-∞, ∞)

10) Decreasing interval

None

Problem 2 :

y = 4^x - 1

a) Describe the transformations to the parent function.

b) What is the asymptote?

c) What is the domain and range?

d) What is the interval of increase/decrease?

e) What are the intercepts?

f) What is the end behavior?

Solution :

y = 4^x - 1

Comparing the given function with parent function y = ab^x

a) The graph of y = 4^x should be moved one unit down to get the graph of y = 4^x - 1.

b) Horizontal asymptote is y = -1

c) Domain is all real values. Range is (-1, ∞)

d) Since it is an exponential growth function (b = 4 > 1), increasing interval is (-∞, ∞).

x-intercept :

Put y = 0

0 = 4^x - 1

4^x = 1

There is no x-intercept.

y-intercept :

put x = 0

y = 4⁰ - 1

y = 1 - 1

y = 0

g) What is the end behavior :

When x --> -∞, then y --> -1

When x --> ∞, then y --> ∞

Problem 3 :

y = 2(1/2)^x

a) Describe the transformations to the parent function.

b) What is the asymptote?

c) What is the domain and range?

d) What is the interval of increase/decrease?

e) What are the intercepts?

f) What is the end behavior?

Solution :

Here a = 2 and b = 1/2 (0 < b < 1)

So, it is exponential decay function.

Since a > 1, vertical stretch will be there.

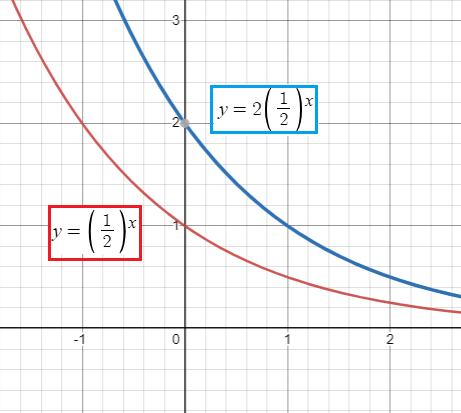
b) Horizontal asymptote is at y = 0

c) Domain is (-∞, ∞) and range (0, ∞).

d) b = 1/2 <1, it is exponential decay and its decreasing interval is at (-∞, ∞).

e) There is no x-intercept and when y = 0, x = 2.

When x --> -∞, then y --> ∞

When x --> ∞, then y --> 0

Problem 4 :

y = 2^-x+ 2

a) Describe the transformations to the parent function.

b) What is the asymptote?

c) What is the domain and range?

d) What is the interval of increase/decrease?

e) What are the intercepts?

Solution :

Here a = 1 and b = 2 (b > 1)

So, it is exponential growth function.

a) Comparing with the parent function y = 2^x, there is reflection across y-axis and move the graph 2 units up.

b) Horizontal asymptote at y = 2

c) Domain is all real values (-∞, ∞) and range (2, ∞).

d) There us no x-intercept and y-intercept is 2.

CHARACTERISTICS OF EXPONENTIAL FUNCTIONS

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling