CHARCTERISTICS OF ABSOLUTE VALUE FUNCTIONS

Find the following and graph it.

(i) Vertex

(ii)  Slope

(iii) y-intercept and x-intercept

(iv) domain and range

(v)  Increasing and decreasing interval.

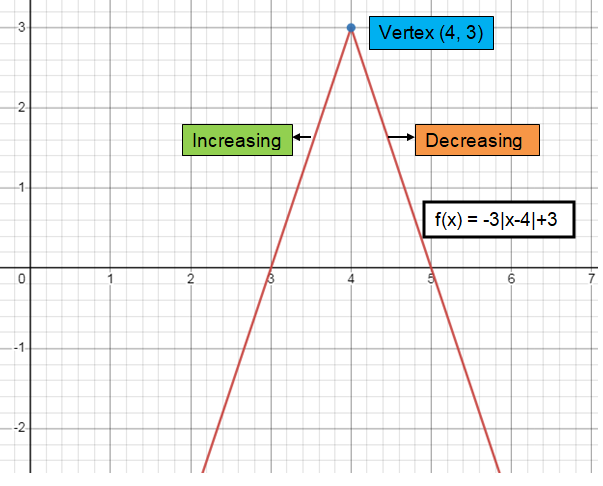
Problem 1 :

f(x) = -3│x - 4│ + 3

Solution :

a = -3, h = 4, k = 3

Vertex:

f(x) = -3│x - 4│ + 3

Comparing with f(x) = a |x - h|+ k

Vertex (h, k) = (4, 3)

Slope :

Slope (a) = -3

The curve will open down.

y- intercept :

y- Intercept, put x = 0

y = -3│0 - 4│ + 3

y = -3(4) + 3

y = -12 + 3

y = -9

y- Intercept is (0, -9)

Zeros :

x- Intercept, put y = 0

 -3│x - 4│ + 3 = 0

-3│x - 4│= -3

│x - 4│= -3/-3

│x - 4│= 1

x = 1 + 4

x = 5

x- Intercept is (5, 0)

Domain and range :

• All real value is domain.
• Range is [3, -∞)

Increasing and decreasing :

• To the left of maximum, it is increasing. (-∞, 4)
• To the right of maximum, it is decreasing. (4, ∞)

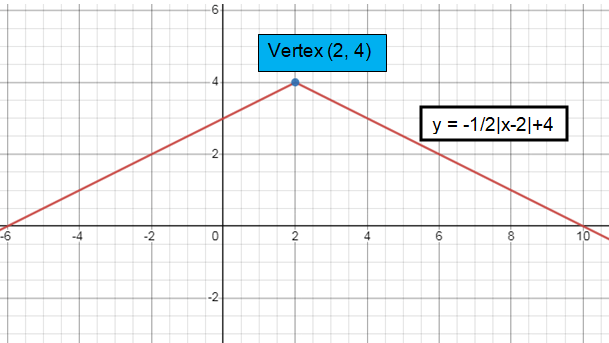
Problem 2 :

f(x) = -1/2│x - 2│ + 4

Solution :

a = -1/2, h = 2, k = 4

Vertex :

f(x) = -1/2│x - 2│ + 4

Comparing with f(x) = a│x - h│+ k

Vertex (h, k) = (2, 4)

Slope :

Slope (a) = -1/2

The curve will open down.

y- intercept :

y- Intercept, put x = 0

y = -1/2│0 - 2│ + 4

y = -1/2(2) + 4

y = -1 + 4

y = 3

y- Intercept = (0, 3)

Zeros :

x- Intercept, put y = 0

 -1/2│x - 2│ + 4 = 0

-1/2│x - 2│= -4

│x - 2│= -4(-2)

│x - 2│= 8

x = 8 + 2

x = 10

x- Intercept is (10, 0)

Domain and range:

• All real value is domain.
• Range is (-∞, 4]

Increasing and decreasing:

• To the left of maximum, it is increasing. (-∞, 2]
• To the right of maximum, it is decreasing. [2, ∞)

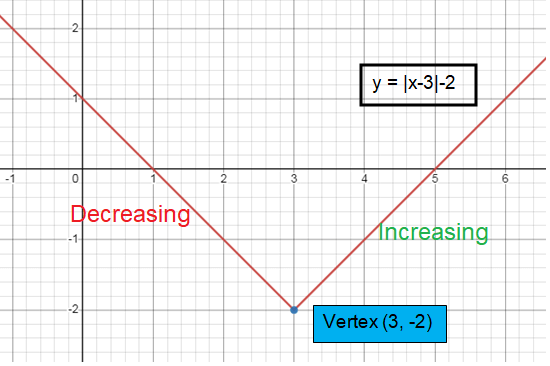
Problem 3 :

f(x) = │x - 3│ - 2

Solution :

a = 1, h = 3, k = -2

Vertex :

f(x) = │x - 3│ - 2

Comparing with f(x) = a│x - h│+ k

Vertex (h, k) is (3, -2)

Slope :

Slope (a) = 1

The curve will open up.

y- intercept :

y- Intercept, put x = 0

y = │0 - 3│ - 2

y = 3 - 2

y = 1

y- Intercept is (0, 1)

Zeros :

x- Intercept, put y = 0

 │x - 3│ - 2 = 0

│x - 3│= 2

x = 2 + 3

x = 5

x- Intercept is (5, 0)

Domain and range :

• All real value is domain.
• Range is [-2, ∞)

Increasing and decreasing :

• To the right of minimum, it is increasing. (∞, 3]
• To the left of minimum, it is decreasing. [3,-∞)

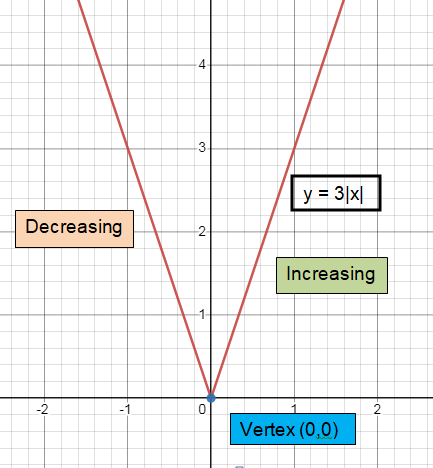
Problem 4 :

f(x) = 3│x│

Solution :

a = 3, h = 0, k = 0

Vertex:

f(x) = 3│x - 0│ + 0

Comparing with f(x) = a│x - h│+ k

Vertex (h, k) = (0, 0)

Slope:

Slope (a) = 3

The curve will open up.

y- intercept:

y- Intercept, put x = 0

y = 3(0)

y = 0

y- Intercept = (0, 0)

Zeros:

x- Intercept, put y = 0

3│x│ = 0

x = 0

x- Intercept = (0, 0)

Domain and range:

• All real value is domain.
• Range is [0, ∞)

Increasing and decreasing:

• To the right of minimum, it is increasing. [0, ∞)
• To the left of minimum, it is decreasing. (-∞, 0]

Problem 5 :

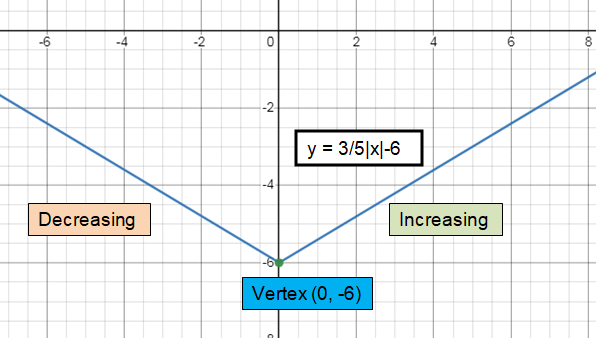
y = 3/5 │x│- 6

Solution :

a = 3/5, h = 0, k = -6

Vertex :

f(x) = 3/5│x - 0│ - 6

Comparing with f(x) = a│x - h│+ k

Vertex (h, k) = (0, -6)

Slope :

Slope (a) = 3/5

The curve will open up.

y- intercept :

y- Intercept, put x = 0

y = 3/5(0) - 6

y = -6

y- Intercept is (0, -6)

Zeros :

x- Intercept, put y = 0

3/5│x│- 6 = 0

3/5 │x│ = 6

x = 10

x- Intercept is (10, 0)

Domain and range :

• All real value is domain.
•  Range is [-6, ∞)

Increasing and decreasing:

• To the right of minimum, it is increasing. (0, ∞)
• To the left of minimum, it is decreasing. (-∞, 0)

Problem 6 :

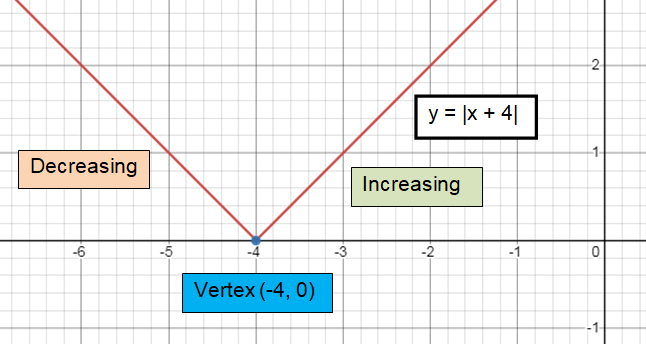
y =│x + 4│

Solution :

a = 1, h = -4, k = 0

Vertex:

f(x) =│x + 4│ + 0

Comparing with f(x) = a│x - h│+ k

Vertex (h, k) is (-4, 0)

Slope:

Slope (a) = 1

The curve will open up.

y- intercept:

y- Intercept, put x = 0

y = │0 + 4│

y = 4

y- Intercept = (0, 4)

Zeros:

x- Intercept, put y = 0

│x + 4│= 0

x = -4

x- Intercept = (-4, 0)

Domain and range:

•  All real value is domain.
• Range is [0, ∞)

Increasing and decreasing:

• To the right of minimum, it is increasing. (-4, ∞)
• To the left of minimum, it is decreasing. (-∞, -4)